|
|
|
|
|
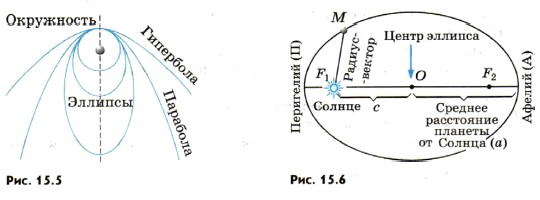
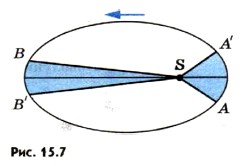
Глава 15. Солнечная система § 117. Законы движения планетВ конце XVI в. датский астроном И. Кеплер, изучая движение планет, открыл три закона их движения. На основании этих законов И. Ньютон вывел формулу для закона всемирного тяготения. В дальнейшем, используя законы механики, И. Ньютон решил задачу двух тел — вывел законы, по которым одно тело движется в поле тяготения другого тела. Он получил три обобщенных закона Кеплера. Первый закон Кеплера. Под действием силы притяжения одно небесное тело движется в поле тяготения другого небесного тела по одному из конических сечений — кругу, эллипсу, параболе или гиперболе (рис. 15.5). Планеты движутся вокруг Солнца по эллиптической орбите (рис. 15.6). Ближайшая к Солнцу точка орбиты называется перигелием, самая далекая — афелием. Линия, соединяющая какую-либо точку эллипса с фокусом, называется радиус-вектором. Отношение расстояния между фокусами к большой оси (к наибольшему диаметру) называется эксцентриситетом е. Эллипс тем сильнее вытянут, чем больше его эксцентриситет. Большая полуось эллипса а — среднее расстояние планеты до Солнца. По эллиптическим орбитам движутся и кометы и астероиды. У окружности е = 0, у эллипса 0 < е < 1, у параболы е = 1, у гиперболы е > 1 (см. рис. 15.5). Движение естественных и искусственных спутников вокруг планет, движение одной звезды вокруг другой в двойной системе также подчиняются этому первому обобщенному закону Кеплера. Второй закон Кеплера. Каждая планета движется так, что радиус-вектор планеты за равные промежутки времени описывает равные площади.
Планета проходит путь от точки А до А' и от В до В' (рис. 15.7) за одно и то же время. Другими словами, планета движется быстрее всего в перигелии, а медленнее всего — когда находится на наибольшем удалении (в афелии). Таким образом, второй закон Кеплера определяет скорость движения планеты. Она тем больше, чем планета ближе к Солнцу. Так, скорость кометы Галлея в перигелии равна 55 км/с, а в афелии 0,9 км/с. Третий закон Кеплера. Куб большой полуоси орбиты тела, деленный на квадрат периода его обращения и на сумму масс тел, есть величина постоянная. Если Т — период обращения одного тела вокруг другого тела на среднем расстоянии а, то третий обобщенный закон Кеплера записывается как а3/[Т2 (М1 + М2)] = G/4π2, (15.2) где М1 и М2 — массы притягивающихся двух тел, a G — гравитационная постоянная. Для Солнечной системы масса Солнца
Правая часть уравнения — постоянная для всех тел Солнечной системы, что и утверждает третий закон Кеплера, полученный ученым из наблюдений. Третий обобщенный закон Кеплера позволяет определять массы планет по движению их спутников, а массы двойных звезд — по элементам их орбит. Движение планет и других небесных тел вокруг Солнца под действием силы тяготения происходит по трем законам Кеплера. Эти законы позволяют рассчитывать положения планет и определять их массы по движению спутников вокруг них. Вопросы к параграфу 1. Перечислите основные элементы эллиптической орбиты планеты. 2. Как связаны периоды обращения планет с их средними расстояниями до Солнца? 3. Сформулируйте первый обобщенный закон Кеплера. 4. Запишите третий обобщенный закон Кеплера.
|
|
|



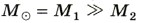 массы любой планеты, и тогда
массы любой планеты, и тогда
