|
|
|
|
|
Глава 4. Электромагнитные колебания § 33. Конденсатор в цепи переменного токаПостоянный ток не может идти по цепи, содержащей конденсатор. Ведь фактически при этом цепь оказывается разомкнутой, так как обкладки конденсатора разделены диэлектриком. Переменный же ток может идти по цепи, содержащей конденсатор. В этом можно убедиться с помощью простого опыта.
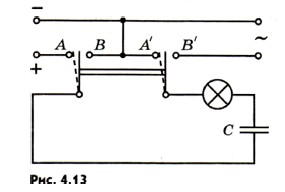
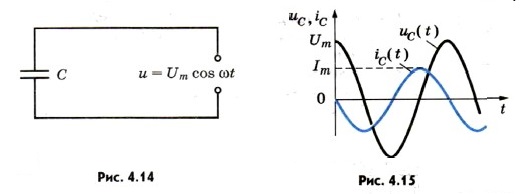
Пусть у нас имеются источники постоянного и переменного напряжений, причем постоянное напряжение на зажимах источника равно действующему значению переменного напряжения. Цепь состоит из конденсатора и лампы накаливания (рис. 4.13), соединенных последовательно. При включении постоянного напряжения (переключатель повернут влево, цепь подключена к точкам АА') лампа не светится. Но при включении переменного напряжения (переключатель повернут вправо, цепь подключена к точкам ВВ') лампа загорается, если емкость конденсатора достаточно велика. Как же переменный ток может идти по цепи, если она фактически разомкнута (между пластинами конденсатора заряды перемещаться не могут)? Все дело в том, что происходит периодическая зарядка и разрядка конденсатора под действием переменного напряжения. Ток, идущий в цепи при перезарядке конденсатора, нагревает нить лампы. Установим, как меняется со временем сила тока в цепи, содержащей только конденсатор, если сопротивлением проводов и обкладок конденсатора можно пренебречь (рис. 4.14). Напряжение на конденсаторе
равно напряжению на концах цепи. Следовательно,
Заряд конденсатора меняется по гармоническому закону: q = CUm cos ωt. Сила тока, представляющая собой производную заряда по времени, равна:
Следовательно, колебания силы тока опережают по фазе колебания напряжения на конденсаторе на Амплитуда силы тока равна: Im = UmCω. (4.29) Если ввести обозначение
и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим
Величину Хс, обратную произведению ωС циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома (см. формулу (4.17)). Действующее значение силы тока связано с действующим значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение для участка цепи постоянного тока. Это и позволяет рассматривать величину Хс как сопротивление конденсатора переменному току (емкостное сопротивление). Чем больше емкость конденсатора, тем больше ток перезарядки. Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора. В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение Хс. С увеличением емкости оно уменьшается. Уменьшается оно и с увеличением частоты ω. В заключение отметим, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода, при разрядке конденсатора, эта энергия возвращается в сеть. Сопротивление цепи с конденсатором обратно пропорционально произведению циклической частоты на электроемкость. Колебания силы тока опережают по фазе колебания напряжения на Вопросы к параграфу 1. Как связаны между собой действующие значения силы тока и напряжения на конденсаторе в цепи переменного тока? 2. Выделяется ли энергия в цепи, содержащей только конденсатор, если активным сопротивлением цепи можно пренебречь? 3. Выключатель цепи представляет собой своего рода конденсатор. Почему же выключатель надежно размыкает цепь?
|
|
|






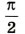 (рис. 4.15).
(рис. 4.15).

