|
|
|
|
|
Глава 8. Световые волны § 67. Интерференция механических волнЛюбому волновому движению присущи явления интерференции и дифракции, с которыми мы начинаем сейчас знакомиться. Для того чтобы убедиться в том, что свет имеет волновую природу, необходимо было найти экспериментальные доказательства интерференции и дифракции света. Чтобы лучше понять явление интерференции света, мы вначале остановимся на интерференции механических волн. Сложение волн. Очень часто в среде одновременно распространяется несколько различных волн. Например, когда в комнате беседуют несколько человек, то звуковые волны накладываются друг на друга. Что при этом происходит? Проще всего проследить за наложением механических волн, наблюдая волны на поверхности воды. Если мы бросим в воду два камня, образовав тем самым две круговые волны, то можно будет заметить, что каждая волна проходит сквозь другую и ведет себя в дальнейшем так, как будто другой волны совсем не существовало. Точно так же любое число звуковых волн может одновременно распространяться в воздухе, ничуть не мешая друг другу. Множество музыкальных инструментов в оркестре или голосов в хоре создает звуковые волны, одновременно улавливаемые нашим ухом. Причем ухо может отличить один звук от другого. Теперь посмотрим более внимательно, что происходит в местах, где волны накладываются одна на другую. Наблюдая волны на поверхности воды от двух брошенных в воду камней, можно заметить, что некоторые участки поверхности не возмущены, в других же местах возмущение усилилось. Если две волны встречаются в одном месте своими гребнями, то в этом месте возмущение поверхности воды усиливается. Если же, напротив, гребень одной волны встречается с впадиной другой, то поверхность воды не будет возмущена. Вообще же в каждой точке среды колебания, вызванные двумя волнами, просто складываются. Результирующее смещение любой частицы среды представляет собой алгебраическую сумму смещений, которые происходили бы при распространении одной из волн в отсутствие другой. Интерференция. Сложение в пространстве волн, при котором образуется постоянное во времени распределение амплитуд результирующих колебаний частиц среды, называется интерференцией1. 1 От латинских слов inter — взаимно, между собой и ferio — ударяю, поражаю. Выясним, при каких условиях наблюдается интерференция волн. Для этого рассмотрим более подробно сложение волн, образующихся на поверхности воды.
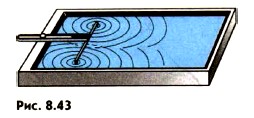
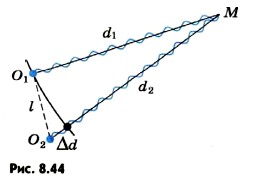
Можно одновременно возбудить две круговые волны в ванне с помощью двух шариков, укрепленных на стержне, которые совершают гармонические колебания (рис. 8.43). В любой точке М на поверхности воды (рис. 8.44) будут складываться колебания, вызванные двумя волнами (от источников O1 и O2). Амплитуды колебаний, вызванных в точке М обеими волнами, будут, вообще говоря, различаться, так как волны проходят различные пути d1 и d2. Но если расстояние l между источниками много меньше этих путей (l « d1 и l « d2), то обе амплитуды можно считать практически одинаковыми.
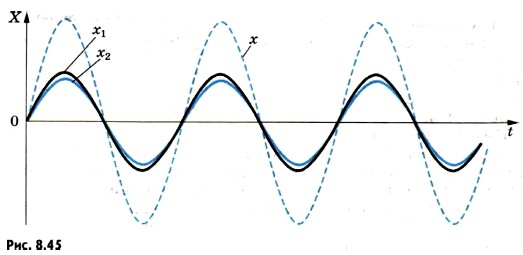
Результат сложения волн, приходящих в точку М, зависит от разности фаз между ними. Пройдя различные расстояния d1 и d2, волны имеют разность хода Δd = d2 - d1. Если разность хода равна длине волны λ, то вторая волна запаздывает по сравнению с первой на один период (именно за период волна проходит путь, равный ее длине волны λ.). Следовательно, в этом случае гребни (как и впадины) обеих волн совпадают. Условие максимумов. На рисунке 8.45 изображена зависимость от времени смещений х1 и х2, вызванных двумя волнами при Δd = λ. Разность фаз колебаний равна нулю (или, что то же самое, 2π, так как период синуса равен 2π). В результате сложения этих колебаний возникают результирующие колебания с удвоенной амплитудой. Колебания результирующего смещения х на рисунке показаны цветной штриховой линией. То же самое будет происходить, если на отрезке Δd укладывается не одна, а любое целое число длин волн.
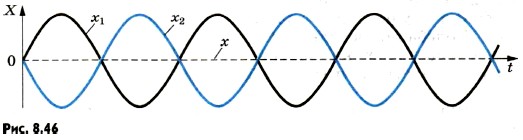
Амплитуда колебаний частиц среды в данной точке максимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна целому числу длин волн: Δd = ±kλ, (8.14) где k = 0, 1, 2, .... Условие минимумов. Пусть теперь на отрезке Ad укладывается половина длины волны. Очевидно, что при этом вторая волна отстает от первой на половину периода. Разность фаз оказывается равной л, т. е. колебания будут происходить в противофазе. В результате сложения этих колебаний амплитуда результирующих колебаний равна нулю, т. е. в рассматриваемой точке колебаний нет (рис. 8.46). То же самое произойдет, если на отрезке укладывается любое нечетное число полуволн. Амплитуда колебаний частиц среды в данной точке минимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна нечетному числу полуволн:
Если разность хода d2 - d1 принимает промежуточное значение между Когерентные волны. Для образования устойчивой интерференционной картины необходимо, чтобы источники волн имели одинаковую частоту и разность фаз их колебаний была постоянной. Источники, соответствующие этим двум условиям, называются когерентными1. Когерентными называют и созданные ими волны. Только при сложении когерентных волн образуется устойчивая интерференционная картина. 1 От латинского слова cohaereus — взаимосвязанный. Если же разность фаз колебаний источников не остается постоянной, то в любой точке среды разность фаз колебаний, возбуждаемых двумя волнами, будет меняться с течением времени. Поэтому амплитуда результирующих колебаний с течением времени будет непрерывно изменяться. В результате максимумы и минимумы перемещаются в пространстве, и интерференционная картина размывается. Распределение энергии при интерференции. Волны несут энергию. Что же с этой энергией происходит при гашении волн друг другом? Может быть, она превращается в другие формы, и в минимумах интерференционной картины выделяется тепло? Ничего подобного! Наличие минимума в данной точке интерференционной картины означает, что энергия сюда не поступает совсем. Вследствие интерференции происходит перераспределение энергии в пространстве. Она не распределяется равномерно по всем частицам среды, а концентрируется в максимумах за счет того, что в минимумы не поступает вовсе. Обнаружение интерференционной картины доказывает, что мы наблюдаем волновой процесс. Волны могут гасить друг друга, а сталкивающиеся частицы никогда не уничтожают друг друга целиком. Интерферируют только когерентные (согласованные) волны. Вопросы к параграфу 1. Какие волны называют когерентными? 2. Что называют интерференцией?
|
|
|




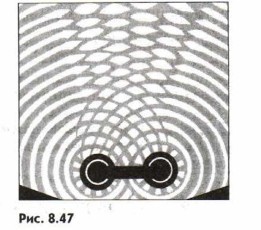
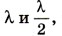 то и амплитуда результирующих колебаний принимает некоторое промежуточное значение между удвоенной амплитудой и нулем. Но важно то, что амплитуда колебаний в любой точке не меняется с течением времени. На поверхности воды возникает определенное, неизменное во времени распределение амплитуд колебаний, которое называют интерференционной картиной. На рисунке 8.47 показана фотография интерференционной картины для двух круговых волн от двух источников (черные кружки). Белые участки в средней части фотографии соответствуют максимумам колебаний, а темные — минимумам.
то и амплитуда результирующих колебаний принимает некоторое промежуточное значение между удвоенной амплитудой и нулем. Но важно то, что амплитуда колебаний в любой точке не меняется с течением времени. На поверхности воды возникает определенное, неизменное во времени распределение амплитуд колебаний, которое называют интерференционной картиной. На рисунке 8.47 показана фотография интерференционной картины для двух круговых волн от двух источников (черные кружки). Белые участки в средней части фотографии соответствуют максимумам колебаний, а темные — минимумам.