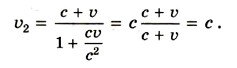|
|
|
|
|
Глава 9. Элементы теории относительности § 78. Основные следствия из постулатов теории относительностиИз постулатов теории относительности вытекает ряд важнейших следствий. Перечислим их, не останавливаясь на обосновании этих следствий. Относительность расстояний. Расстояние между двумя точками тела не является абсолютной величиной, а зависит от скорости движения тела относительно данной системы отсчета. Обозначим через l0 длину стержня в системе отсчета К1, относительно которой стержень покоится. Тогда длина l этого стержня в системе отсчета К, относительно которой стержень движется со скоростью
Как видно из этой формулы, l < l0. В этом состоит так называемое релятивистское сокращение размеров движущегося тела. Относительность промежутков времени. Пусть интервал времени между двумя событиями, происходящими в одной и той же точке инерциальной системы отсчета К, равен τ0. Этими событиями, например, могут быть два удара метронома в K-системе, отсчитывающего секунды. Тогда интервал τ между теми же событиями в системе отсчета К1, движущейся относительно системы К со скоростью
Очевидно, что τ > τ0. В этом состоит релятивистский эффект замедления времени в движущихся системах отсчета: движущиеся часы «тикают» медленнее, чем покоящиеся. Если υ « с, то в формулах (9.1) и (9.2) можно пренебречь величиной Релятивистский закон сложения скоростей. Новым релятивистским представлениям о пространстве и времени соответствует новый закон сложения скоростей. Очевидно, что классический закон сложения скоростей не может быть справедливым, так как он противоречит утверждению о постоянстве скорости света в вакууме. Если поезд движется со скоростью
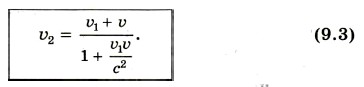
Мы запишем этот закон сложения скоростей для частного случая, когда тело движется вдоль оси Х1 системы отсчета К1, которая, в свою очередь, движется со скоростью Обозначим скорость тела относительно системы отсчета К1 через υ1, а скорость этого же тела относительно системы К через υ2. Тогда релятивистский закон сложения скоростей будет иметь вид:
Если υ « с и υ1 « с, то членом υ2= υ1 + υ. При υ1 = с скорость υ2 также равна с — в соответствии со вторым постулатом теории относительности. Действительно,
Замечательным свойством релятивистского закона сложения скоростей является то, что при любых скоростях υ1 и υ (конечно, не больших с) результирующая скорость υ2 не превышает с. Из постулатов теории относительности следует, что длина тела, промежуток времени между двумя событиями зависят от выбранной системы отсчета, т. е. являются относительными. Релятивистский закон сложения скоростей переходит в классический при υ « с. Вопросы к параграфу 1. При каких скоростях движения релятивистский закон сложения скоростей переходит в классический (закон Галилея)? 2. В чем принципиальное отличие скорости света от скоростей движения тел?
|
|
|



 , определяется формулой
, определяется формулой


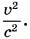 Тогда l ≈ l0 и τ ≈ τ0, т. е. релятивистское сокращение размеров тела и замедление времени в движущихся системах отсчета можно не учитывать.
Тогда l ≈ l0 и τ ≈ τ0, т. е. релятивистское сокращение размеров тела и замедление времени в движущихся системах отсчета можно не учитывать.
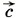 , а не
, а не 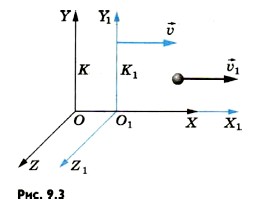
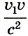 в знаменателе можно пренебречь, и вместо выражения (9.3) получим привычный нам классический закон сложения скоростей:
в знаменателе можно пренебречь, и вместо выражения (9.3) получим привычный нам классический закон сложения скоростей: