|
|
|
|
|
§ 22. Выталкивающая сила. Закон Архимеда Закон Архимеда. Выталкивающая силаР е ш е н и е. Пусть глубина, на которой находится верхнее основание бруска, равна а (рис. 22.4). Силы давления жидкости, действующие на боковые грани бруска, взаимно уравновешиваются. На верхнее основание бруска действует сила давления Присмотримся снова к полученному ответу. Мы увидим, что на этот раз сила Архимеда равна по модулю весу жидкости в объёме всего бруска. Действительно, произведение dS равно объёму бруска, ρжdS равно массе жидкости в объёме бруска и, наконец, ρжgdS равно весу жидкости в объёме бруска. Вспомним теперь, что, когда брусок был погружён в воду частично, сила Архимеда равнялась весу жидкости в объёме погружённой части бруска. Теперь мы можем обобщить этот вывод и на тот случай, когда погружённой частью является весь брусок. Можно доказать, что полученный вывод справедлив для тела любой формы. Это доказательство, не требующее вычислений, приведено в разделе «Доказательство закона Архимеда для тела произвольной формы». Таким образом,
Впервые это установил на опыте Архимед, поэтому это утверждение называют законом Архимеда. Напомним, что для полностью погружённого тела «погружённой частью тела» следует считать всё тело. О красивом опыте, подтверждающем закон Архимеда, рассказано в разделе «Ведёрко Архимеда».
|
|
|



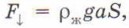 направленная вниз, а на нижнее основание — сила давления
направленная вниз, а на нижнее основание — сила давления 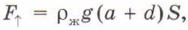 направленная вверх. Равнодействующая этих сил и есть сила Архимеда
направленная вверх. Равнодействующая этих сил и есть сила Архимеда 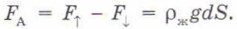
 Чему равна сила Архимеда, действующая на полностью погружённый в воду куб с длиной ребра 10 см? Чему будет равна эта сила, если куб погружён наполовину?
Чему равна сила Архимеда, действующая на полностью погружённый в воду куб с длиной ребра 10 см? Чему будет равна эта сила, если куб погружён наполовину?