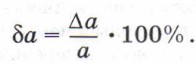Книги и учебники онлайн

Точность измерений

2. Как правильно записать результат измерений с учётом абсолютной погрешности?

Для ответа на этот вопрос рассмотрим пример. Измерим длину стола I с помощью демонстрационного метра, цена деления которого 1 см. Она будет равна 231 см. Абсолютная погрешность измерения составляет половину цены деления, следовательно, она равна 0,5 см. Тогда результат измерения длины стола запишется в виде:

l = (231,0 ± 0,5) см.

Это означает, что истинное значение измеряемой величины лежит в пределах:

230,5 см ≤ l ≤ 231,5 см.

На числовом луче (рис. 17) выделен интервал, в котором находится истинное значение длины стола; ширина этого отрезка равна 1 см.

Таким образом, если значение физической величины А, полученное в результате измерения, обозначить через а, абсолютную погрешность измерения через Δа (Δ — греч. буква «дельта»), то результат измерения запишется так:

А = а ± Δа.

Для того чтобы узнать, насколько велика погрешность измерения в каждом случае, вычисляют относительную погрешность δа. Она равна отношению абсолютной погрешности Δа к значению а физической величины, полученному в результате измерения:

Вопросы для самопроверки

1. Можно ли физическую величину измерить точно? Ответ поясните.

2. Назовите причины погрешностей при измерении.

3. Как связана точность измерений с ценой деления шкалы прибора?

4. Как записать результат измерений с учётом погрешности?

Задание

1_Э. Измерьте с помощью линейки длину тетради и запишите результат с учётом погрешности измерения.

2. Запишите показания приборов, изображённых на рисунках 11—14, с учётом погрешности измерения.

<<< К началу