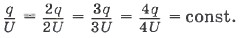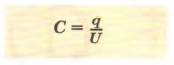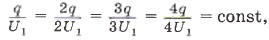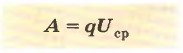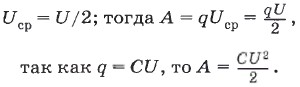Главная >> Физика 8 класс. Перышкин. Онлайн учебник

Глава 2. Электрические явления

§ 54. Конденсатор

Как вам известно, вокруг заряженных тел существует электрическое поле, которое обладает энергией.

А можно ли накапливать заряды и энергию электрического поля? Устройством, позволяющим накапливать заряды, является конденсатор (от лат. condensare — сгущение). Простейший плоский конденсатор состоит из двух одинаковых металлических пластин — обкладок, находящихся на небольшом расстоянии друг от друга и разделённых слоем диэлектрика, например воздуха (рис. 83). Толщина диэлектрика в сравнении с размерами обкладок небольшая.

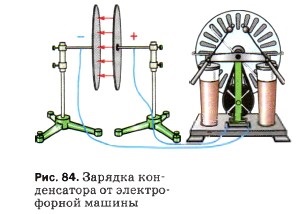
Продемонстрируем на опыте способность конденсатора накапливать заряды. Для этого две металлические пластины подключим к разным полюсам электрофорной машины (рис. 84). Пластины получат одинаковые по модулю, но разные по знаку заряды. Возникнет электрическое поле. Электрическое поле конденсатора практически сосредоточено между пластинами внутри конденсатора.

После отключения электрофорной машины заряды на пластинах и электрическое поле между ними сохранятся.

Если обкладки заряженного конденсатора соединить проводником, то по проводнику некоторое время будет проходить ток. Значит, заряженный конденсатор является источником тока.

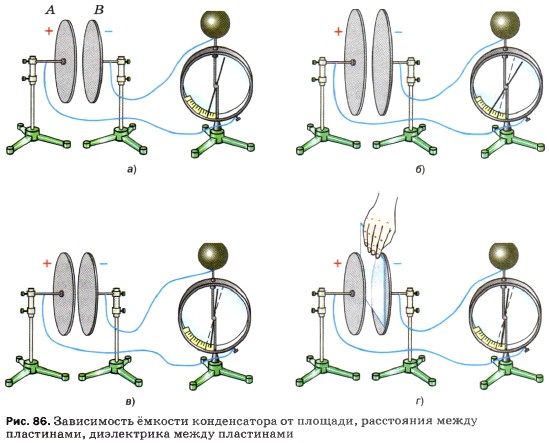
В зависимости от диэлектрика конденсаторы бывают нескольких типов: с твёрдым, жидким и газообразным диэлектриком. Их различают и по форме обкладок: плоские, цилиндрические, сферические и др. (рис. 85).

Свойство конденсатора накапливать электрические заряды характеризуется электроёмкостью, или ёмкостью. Для того чтобы понять, от чего зависит эта физическая величина, обратимся к опыту.

Две металлические пластины, укреплённые на изолирующих подставках параллельно друг другу, соединим с электрометром. Одну из пластин соединим со стержнем электрометра, другую заземлим, соединив с корпусом прибора (рис. 86, а). Наэлектризованным шаром коснёмся внешней стороны пластины А, тем самым сообщив ей положительный заряд +q. Под действием электрического поля пластины А в пластине В произойдёт перераспределение зарядов: отрицательные заряды расположатся на внутренней стороне пластины. С земли придут свободные электроны, чтобы нейтрализовать положительные заряды на внешней стороне пластины В. Таким образом, на пластине В возникнет равный по величине отрицательный заряд -q.

Стрелка электрометра отклонится от нулевого положения. С помощью одинаково заряженных шаров продолжим передавать конденсатору заряды последовательно равными порциями. Мы заметим, что при увеличении заряда в 2, 3, 4 раза соответственно в 2, 3, 4 раза увеличатся показания электрометра, т. е. увеличится напряжение между пластинами конденсатора. Причём отношение заряда к напряжению будет оставаться постоянным:

• Величина, измеряемая отношением заряда одной из пластин конденсатора к напряжению между пластинами, называется электроёмкостью конденсатора.

Электроёмкость конденсатора вычисляется по формуле:

За единицу ёмкости в СИ принимается фарад (Ф), название дано в честь английского физика Майкла Фарадея. Электроёмкость конденсатора равна единице, если при сообщении ему заряда 1 Кл возникает напряжение 1 В.

1 Ф — это очень большая ёмкость, поэтому на практике используют микрофарад (мкФ) и пикофарад (пФ).

1 мкФ = 10^-6 Ф; 1 пФ = 10^-12 Ф.

Выясним, от чего зависит ёмкость кондеса- тора. Для этого возьмём конденсатор с пластинами, имеющими большую площадь (рис. 86, б). Повторим опыт. Отношение заряда к напряжению и в этом случае остаётся постоянным

но отношение заряда к напряжению теперь больше, чем в первом опыте, т. е. С₁ > С. Чем больше площадь пластин, тем больше ёмкость конденсатора.

Ещё раз проделаем первый опыт, но теперь изменим расстояние между пластинами (рис. 86, в). С уменьшением расстояния между пластинами уменьшается напряжение между ними. При уменьшении расстояния между пластинами конденсатора при неизменном заряде ёмкость конденсатора увеличивается.

Проделаем ещё один опыт. Установим пластины конденсатора А и Б на некотором расстоянии друг от друга. Пластину А зарядим. Заметим показания электрометра, когда между пластинами находится воздух. Разместим между пластинами лист из оргстекла или другой диэлектрик (рис. 86, г). Мы заметим, что напряжение между пластинами уменьшится. Следовательно, ёмкость конденсатора зависит от свойств внесённого диэлектрика.

При внесении диэлектрика ёмкость конденсатора увеличивается.

Конденсатор, как и любое заряженное тело, обладает энергией. Проверим это на опыте. Зарядим конденсатор и подсоединим к нему электрическую лампочку. Лампочка ярко вспыхнет. Это свидетельствует о том, что заряженный конденсатор обладает энергией. Энергия конденсатора превращается во внутреннюю энергию нити накаливания лампы и проводов.

Для того чтобы зарядить конденсатор, нужно было совершить работу по разделению положительных и отрицательных зарядов. В соответствии с законом сохранения энергии, совершённая работа А равна энергии конденсатора E, т. е.

А = Е,

где Е — энергия конденсатора.

Работу, которую совершает электрическое поле конденсатора, можно найти по формуле:

где U_ср — это среднее значение напряжения.

Поскольку в процессе разрядки напряжение не остаётся постоянным, необходимо найти среднее значение напряжения:

Значит, энергия конденсатора ёмкостью С будет равна:

Конденсаторы могут длительное время накапливать энергию, а при разрядке они отдают её почти мгновенно. Свойство конденсатора накапливать и быстро отдавать электрическую энергию широко используется в электротехнических и электронных устройствах, в медицинской технике (рентгеновская техника, устройства электротерапии), при изготовлении дозиметров, аэрофотосъёмке.

Вопросы

1. Для чего служат конденсаторы?
2. Что характеризует электроёмкость конденсатора?
3. Что принято за единицу электроёмкости в СИ?
4 От чего зависит электроёмкость конденсатора?

Упражнение 38

1. Пластины плоского конденсатора подсоединяют к источнику напряжения в 220 В. Ёмкость конденсатора равна 1,5 • 10^-4 мкФ. Чему будет равен заряд конденсатора?

2. Заряд плоского конденсатора равен 2,7 10^-2Кл, его ёмкость 0,01 мкФ. Найдите напряжение между обкладками конденсатора.

Задание

1. Используя Интернет, найдите, как был устроен первый конденсатор — лейденская банка. Изготовьте её.

2. Подготовьте выступление об истории создания конденсатора.