Понятия простого и сложного процентов

Использование в расчетах сложного процента в случае многократного его начисления более логично, поскольку в этом случае капитал, генерирующий доходы, постоянно возрастает. При применении простого процента доходы по мере их начисления целесообразно снимать для потребления или использования в других инвестиционных проектах или текущей деятельности.

Итак, формула наращения по схеме сложных процентов имеет вид

формула наращения по схеме сложных процентов имеет вид

Множитель FM1(r, n) = (1 + r)ⁿ инвариантен по отношению к суммовым величинам, а потому для удобства пользования его можно табулировать для различных комбинаций r и n (см. Приложение 3), Этот множитель называется мультиплицирующим множителем для единичного платежа. Формула сложных процентов является одной из базовых формул в финансовых вычислениях.

Экономический смысл множителя FM1(r, n): он показывает, чему будет равна одна денежная единица (один рубль, один доллар, одна иена и т. п.) через n периодов при заданной процентной ставке r, т. е. он оценивает будущую стоимость одной денежной единицы. Подчеркнем, что при пользовании этой и последующими финансовыми таблицами необходимо следить за соответствием длины периода и процентной ставки. Так, если базисным периодом начисления процентов является квартал, то в расчетах должна использоваться квартальная ставка.

В практических расчетах для наглядной и быстрой оценки эффективности предлагаемой ставки наращения при реализации схемы сложных процентов пользуются приблизительным расчетом времени, необходимого для удвоения инвестированной суммы, известным как правило 72-х. Это правило заключается в следующем; если r — процентная ставка, выраженная в процентах, то 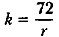представляет собой число периодов, за которое исходная сумма приблизительно удвоится. Это правило хорошо срабатывает для небольших значений r (до 20%). Так, если годовая ставка r = 12%, то k = 6 годам. Подчеркнем, что здесь речь идет о периодах начисления процентов и соответствующей данному периоду ставке. Если базисным периодом, т. е, периодом наращения, является половина года, то в расчете должна использоваться полугодовая ставка. Следует также обратить внимание на то, что хотя в большинстве финансовых расчетов процентная ставка берется в долях единицы, в формуле алгоритма правила 72-х ставка взята в процентах.

<<< К началу