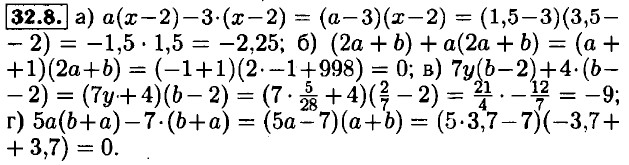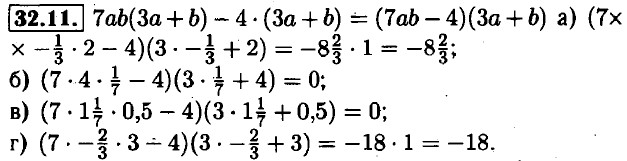|
|
|
|
Главная >> Домашние работы к учебнику Мордкович. Алгебра 7 класс |
|
|
Глава 7. Разложение многочленов на множители Способ группировки32.1. а) (2х - х2; 4ху - 2х2у); 2х - х2; б) (аb - 3b2; а2 - 3аb); а - 3b; в) (n2 - nm; mn - n2); n - m; (6а2 - 9аb - 3b2); 2а - 3b; г) (4х - 8; х2 - 2х); х - 2; (-5 - 15n; 21mn + 7n); m + 1. 32.2. a) (2by - bz; 2ay - az); (4ax - az; 4bх - bz); б) (6ах - 3х; -2а + 1); (3bу - 3у; с - сb); в) (а3 - 2а2; 3а - 6); (4аb - 2а2b; 5ас2 - 10ас); г) ((3mn2 - 6m2n; аbn - 2аbm); (а2х3 - 9а2х; 9х2 - х4). 32.3. а) 3 • (а + 1) + n(а + 1) = (1 + n)(а + 1); б) 3х(2m + 3) - (2m + 3) = (3х - 1)(2m + 3); в) х(а + 3) + 4 • (а + 3) = (х + 4)(а + 3); г) m(2х - 3) + 2 • (2х - 3) = (m + 2)(2х - 3). 32.4. а) k(7n - 6) - 2 • (7n - 6) = (k - 2)(7n - 6); б) 7 • (х + а) - 5а(х + а) = (7 - 5а)(х + а); в) 9m(m - n) - 5 • (m - n) = (9m - 5)(m - n); г) с(b + 3а) - 2а(b + 3а) = (с - 2а)(b + 3а). 32.5. а) у2 • (у + 5) + (у + 5) = (у2 + 1)(у + 5); б) у2 • (у - 2) + 2 • (у - 2) = (у2 + 2)(у - 2); в) z2 • (z + 7) + 3 • (z + 7) = (z2 + 3)(z + 7); г) z2 • (z - 3) + (z - 3) = (z2 + 1 )(z - 3). 32.6. a) 7 • (c2 + 1) - c(c2 + 1) = (7 - c)(c2 + 1); 6) x(x2 - 2) - 14• (x2 - 2) = (x - 14)(x2 - 2); в) x2 • (x - 3) + 2 • (x - 3) = (x2 + 2)(x - 3); г) 2b2 • (b - 2) + 3 • (b - 2) = (2b2 + 3)(b - 2). 32.7. a) 5c(b2 + 2c2) + 16a(b2 + 2c2) = (5c + 16a)(b2 + 2c2); 6) 2n(10n - 7a) + 5 • (10n - 7a) = (2n + 5)(10n - 7a); в) 9a(2a + 3b) + 7c(2a + 3b) = (9a + 7c)(2a + 3b); г) xz(2xy - 3z) + 5y(2xy - 3z) = (xz + 5y)(2xy - 3z).
32.9. a) 8ac(5a2b - 7c) - 3b(5a2b - 7c) = (8a - 3b)(5a2b - 7c); 6) 16x(y2 + 2z2) - 5z(y2 + 2z2) = (16x - 5z)(y2 +2z2); в) 5x(6x - 5c) - 2 • (6x - 5c) = (5x - 2)(6x - 5c); г) 18xz(x - 2k) - 10ky(x - 2k) - (18xz - 10ky)(x - 2k). 32.10. a) x2 • (a - b - c) - y(a - b - c) = (x2 - y)(a - b - c); б) y2 • (x - b + 1) - a(x - b + 1) = (y2 - a)(x - b + 1); в) x(a + b + c) + y(a + b + c) = (x + y)(a + b + c); г) ab( 1 - ab + a2b2) - c(1 - ab + a2b2) = (ab - c)(1 - ab + a2b2).
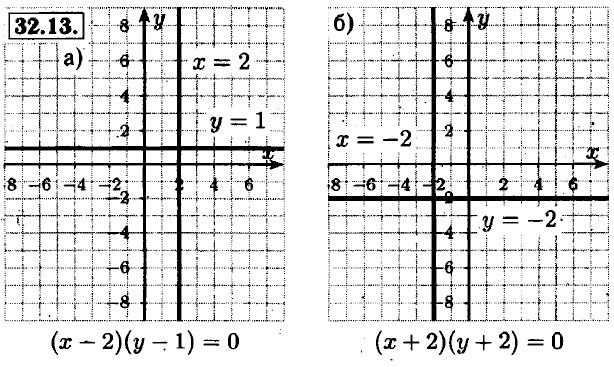
32.12. a) x2 • (x + 2) + 3 • (x + 2) = 0; (x2 + 3)(x + 2) = 0; x = -2;
<<< К началу Решенния (окончание) >>>
|
|
|