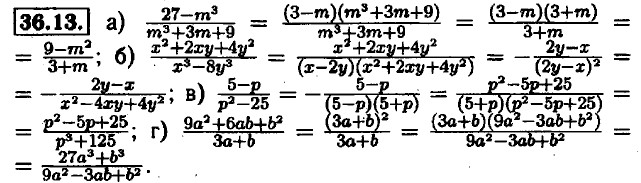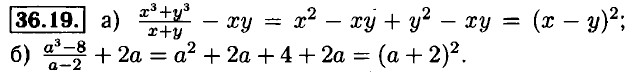Тождества

36.1. а) да; б) да; в) да; г) да.

36.2. а) да; б) да; в) да; г) да.

36.3. а) да; б) да; в) да; г) да.

36.4. а) переместительный закон сложения; б) сочетательный закон сложения; в) переместительный закон умножения; г) распределительный закон сложения относительно умножения.

36.5. а) переместительный и сочетательный законы умножения; б) если из числа а вычесть это же число то в результате получится 0; в) переместительные законы сложения и умножения; г) сочетательный закон умножения и распределительный закон сложения относительно умножения.

36.6. а) х - у = -у + х = -(у - х); б) (m - n)² = (n - m)²; в) 2а - 3b = -3b + 2а = -(3b - 2a); г) (3c - 4d)² = (4d - 3c)².

З6.7 а) 10a - (-(5a + 20)) = 10a + 5 • (a + 4) = 5 • (2a + а + 4) = 5 • (3a + 4); б) -(-7x) - (6x + 5) = 7х - 6 - 5х = 2 • (х - 3); в) 12у - (25 - (6у - 11)) = 12у - 36 + 6у = 18 • (у - 2); г) 36 - (-(9с - 15)) = 36 + 9с - 15 = 3 • (3с + 7).

36.8. а) а² + 7а + 10 = а(а + 5) + 2 • (а + 5) = (а + 2)(а + 5); б) x² - 9x + 20 = х(х - 4) - 5 • (х - 4) = (x - 4)(x - 5); в) (b - 8)(b + 3) = b² - 8b + 3b - 24 = b² - 5b - 24; г) (с - 4)(с + 7) = с² - 4с + 7с - 28 = с² + 3с — 28.

36.9. а) (а - 4)(а + 2) + 4 = а² - 4а + 2а - 8 + 4 = а² + а - 3а -3 - 1 = а(а +1) - 3 • (а + 1) - 1 = (a - 3)(а +1) - 1; б) 16 - (x + 3)(x + 2) = 4 + 12 - х² - 5x - 6 = 4 - (x(x -1) + 6 • (x - 1)) = 4 - (x + 6)(x - 1); в) (у - 3)(у + 7) - 13 = у²- 3у + 7у - 21 - 13 = (у² + 8у - 4у - 32) - 2 = (у + 8)(у - 4) - 2; г) (z - 11)(z + 10) + 10 = z² - 11z + 10z - 110 + 10 = (z² - z - 20) - 80 = (z - 5)(z + 4) - 80.

36.10. a) (а+b)² + (а - b)² = а² + 2аb + b² + а² - 2ab + b² = 2 • (a² + b²); 6) (a + b)² - (a - b)² = a² + 2ab + b² - a² + 2ab - b² = 4ab; в) a² + b² = a² + 2ab + b² - 2ab = (a + b)² - 2ab; г) (a + b)2 - 2b(a + b) = a² + 2ab + b - 2ba - 2b² = a² - b².

36.11. 2x - 1 + 3x + 1 - 5x = 5x - 5x = 5z - 3x - 2x = = 5s - 3x - 1 - 2x + 1 = 5x - (3x + 1) - (2x - 1).

36.12. а) да; x ≠ 0; x ≠ 2; б) да; x ≠ 0; x ≠ 2; в) да; а ≠ 0; а ≠ 3; г) да; а ≠ 0; а ≠ 3; b ≠ 0.

36.14. а) (x + у)(x - у) + (у + а) (у - а) = x² - у² + у2 - а² = (x - а)(x + а); б) (x + а)(x + b) = x² + аx + bx + ab = x² + (а + b)x + аb; в) (а - b)(а + b) - (а - с)(а + с) - (с - b)(с + b) = а² - b² - а²+ c² - с² + b² = 0; г) (m - a)(m - b) = m² - am - bm + ab = m² - (а + b)m + аb.

36.15. (а + 1)(b +1) - (а - 1)(b - 1) = aб + а + b + 1 - ab + а + b - 1 = 2 • (а + b) = 18.

36.16. с² - b² - 2ас + 2аb + а² - с² - 2аb + 2bс - a² + b + 2ас - 2bс = -2ас + 2аb - 2аb + 2bс + 2ас - 2bс = 0.

36.17. а) (2а - b)(2а + b) + (b + с)(b - с) + (с - 2а)(с + 2а) = 4а² - b² + b² - с² + с² - 4а² = 0;
б) (3x + у)2 - (3x - у)² = (3x + у - 3x + у)(3x + у3x - у) = 12xу = 9x²у² + бxу + 1 - 9x²у² + бxу - 1 = (3xу + 2)² - (3xу - 2)²;
в) (x - 3у)(x + 3у) + (3у - с)(3у + с) + (с - x)(с + x) = x² - 9у² + 9у² - с² + с² - x² = 0;
г) (а - b)(а + b)((а - b)² + (а + b)²) = (а² - b²)(2а² + 2b²) = 2 • (а⁴ - b⁴).

36.18. a) (а - 1)³ - 4 • (а - 1) = (а - 1)((а - 1)² - 4) = (а - 1)(а - 3)(а + 1);
б) (x² + 1)² - 4x² = (x² - 2x + 1)(x² + 2x + 1) = (x - 1)² • (x + 1)²;
в) (а + 1)³ - (а +1) = (а + 1)((а + 1)2 - 1) = а(а + 1)(а + 2);
г) 462с2 - (b² + с² - а²)² = (2bс - b² - с² + а²)(2bс + b² + с² - а²) = (а - b + с)(а + b - с)(b + с - а)(а + b + с).

<<< К началу