|
|
|
|
|
§ 7. Степень и ее свойства Определение степени с натуральным показателемПроизведение нескольких одинаковых множителей молено записать в виде выражения, называемого степенью. Например: 5 • 5 • 5 • 5 • 5 • 5 • 5 = 57. Повторяющийся множитель называют основанием степени, а число повторяющихся множителей — показателем, степени. Так, в выражении 57 число 5 — основание степени, а число 7 — показатель степени.
Запись аn читается так: «а в степени n», «n-я степень числа а». Но определению степени а1 = а, а2 = аа, а3 = ааа, а4 = аааа. Вообще
Нахождение значения степени называют возведением в степень. Приведём примеры возведения в степень: 34 = 3-3-3-3 = 81; 02 = 0. (-6)3 = (-6) • (-6) • (-6) = -216; 91 = 9.
При возведении в степень отрицательного числа может получиться как положительное число, так и отрицательное. Например: (-2)1 = -2; (-2)2 = (-2) • (-2) = 4; (-2)3 = (-2) • (-2) • (-2) = -8; (-2)4 = (-2) • (-2) • (-2) • (-2) = 16.
Действительно, произведение чётного числа отрицательных множителей положительно, а произведение нечётного числа отрицательных множителей отрицательно.
При вычислении значений числовых выражений, не содержащих скобки, принят следующий порядок действий: сначала выполняют возведение в степень, затем умножение и деление, далее сложение и вычитание. Вычислим значения нескольких выражений, содержащих степени. Пример 1. Найдём значение выражения 4 • 103.
Значит, 4 • 103 = 4000. Пример 2. Найдём значение выражения -26 + (-3)4.
Значит, -26 + (-3)4 = 17. Рассмотрим теперь, как находят значение степени с помощью калькулятора. IIример 3. Найдём с помощью калькулятора значение степени 2,75.
Однако калькулятор позволяет вычислять значение степени проще, не набирая повторно основание степени и знак умножения. В нашем примере достаточно ввести число 2,7, нажать клавишу
В результате вычислений найдём, что 2,75 = 143,48907.
|
|
|



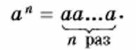
 1) 103 = 10 • 10 • 10 = 1000; 2) 4 • 1000 = 4000.
1) 103 = 10 • 10 • 10 = 1000; 2) 4 • 1000 = 4000.

 и 4 раза нажать клавишу
и 4 раза нажать клавишу  . Получим более удобную схему вычислений:
. Получим более удобную схему вычислений:
