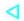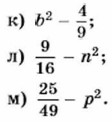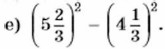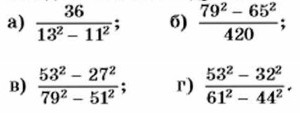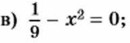Разложение разности квадратов на множители

В тождестве (а - b)(а + b) = а² - b² поменяем местами правую и левую части. Получим

а² - b² = (а - b)(а + b).

Это тождество называют формулой разности квадратов. Её применяют для разложения на множители разности квадратов любых двух выражений:

разность квадратов двух выражений равна произведению разности зтих выражений и их суммы.

Приведём примеры применения формулы разности квадратов.

Пример 1. Разложим на множители выражение 36 -а².

Так как 36 = 6², то

36 - а² = 6² - а² = (6 - а) (6 + а).

Пример 2. Представим в виде произведения двучлен 49х² - 16у⁶.

Данный двучлен можно представить в виде разности квадратов.

Получим

49х² - 16у⁶ = (7х)² - (4у³)² = (7х - 4у³)(7х + 4у³).

Упражнения

883. Разложите на множители многочлен:

а) х² - у²;
б) с² - z²;
в) а² - 25;
г) m² - 1;
д) 16 - b²;
е) 100 - x²;

ж) р²- 400;
з) у² - 0,09;
и) 1,44 - а²;

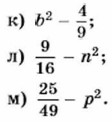
884. Разложите на множители:

а) 25х² - у²;
б) -m² + 16n²;
в) 36а² - 49;
г) 64 - 25х²;

д) 9m² - 16n²;
е) 64р² - 81q²;
-49а² + 16b²;
з) 0,01n² - 4m²;

и) 9 - b²с²;
к) 4а²b² - 1;
л) р² - а²b²;
м) 16c²d² - 9а².

885. Представьте в виде произведения:

а) х² - 64;
б) 0,16 - с²;
в) 121 - m²;

г) -81 + 25у²;
д) 144b² - с²;
е) 0,64х² - 0,49y²;

ж) х²y² - 0,25;
з) с²d² - а²;
и) а²х² - 4у².

886. Вычислите:

а) 47² - 37²;
б) 53² - 63²;
в) 126² - 74²;

г) 21,3² - 21,2²;
д) 0,849² - 0,151²;

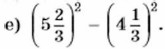
887. Найдите значение дроби:

888. Найдите значение выражения:

а) 41² — 31²;
б) 76² - 24²;
в) 256² - 156²;

г) 0,783² - 0,217²;

889. Разложите на множители:

а) х⁴ - 9;
б) 25- n⁶;
в) m⁸ - а²;
г) у² - р⁴;

д) с⁶ - d⁶;
е) х⁶ - а⁴;
ж) b⁴ - y10;
з) m⁸ - n⁶;

и) а⁴ - b⁴;
к) с⁸ - d⁸;
л) а⁴ - 16;
м) 81 - b⁴.

890. Решите уравнение:

а) х² - 16 = 0;
б) у² - 81 = 0;

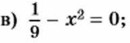
г) а² - 0,25 = 0;
д) b² + 36 = 0;
е) х² - 1 = 0;

ж) 4х² - 9 = 0;
з) 25х² - 16 = 0;
и) 81х² + 4 = 0.

Окончание >>>