|
|
|
|
|
7. Законы движения планет и искусственных небесных тел 1. Форма орбиты и скорость движенияЧем ближе планета к Солнцу, тем, больше ее линейная и угловая скорости и короче период обращения вокруг Солнца. Мы наблюдаем планеты с Земли, которая сама обращается вокруг Солнца. Это движение Земли необходимо учитывать, чтобы узнать периоды обращения планет в невращающей- ся инерциальной системе отсчета, или, как часто говорят, по отношению к звездам. Период обращения планет вокруг Солнца по отношению к звездам называется звездным или сидерическим периодом. Наименьший звездный период обращения у планеты Меркурий — 88 сут. У Марса он составляет почти 2 года, а у Юпитера — 12 лет и, все возрастая с удалением от Солнца, у Плутона доходит почти до 250 лет. Заслуга открытия законов движения планет принадлежит выдающемуся немецкому ученому Иоганну Кеплеру. В начале XVII в. Кеплер установил три закона движения планет. Они названы законами Кеплера.
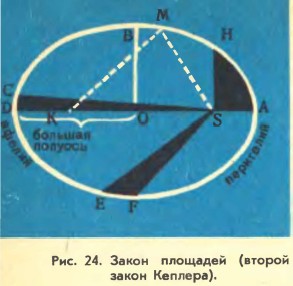
Первый закон Кеплера: каждая планета обращается по эллипсу, в одном из фокусов которого находится Солнце (рис. 24).
Эллипсом (рис. 24) называется плоская замкнутая кривая, имеющая такое свойство, что сумма расстояний каждой ее точки от двух точек, называемых фокусами, остается постоянной. Эта сумма расстояний равна длине большой оси DA эллипса (рис. 24). Точка О — центр эллипса, К и S — фокусы. Солнце находится в данном случае в фокусе S. DO = ОА = а — большая полуось эллипса. Большая полуось а является средним расстоянием планеты от Солнца: Ближайшая к Солнцу точка орбиты А называется перигелием, а самая далекая от него точка D называется афелием. Степень вытянутости эллипса характеризуется его эксцентриситетом е. Эксцентриситет равен отношению расстояния фокуса от центра (ОK = OS) к длине большой полуоси a, т. е. Орбиты планет — эллипсы, мало отличающиеся от окружностей, их эксцентриситеты малы. Например, эксцентриситет орбиты Земли e = 0,017.
|
|
|




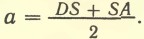
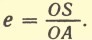 При совпадении фокусов с центром (е = 0) эллипс превращается в окружность.
При совпадении фокусов с центром (е = 0) эллипс превращается в окружность.