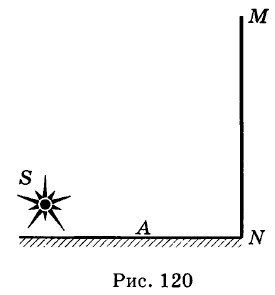
Дисперсия света. Интерференция, дифракция, поляризация света

1078(1046). Какие частоты колебаний соответствуют крайним красным (λ = 0,76 мкм) и крайним фиолетовым (λ = 0,4 мкм) лучам видимой части спектра?

1079(1047). Сколько длин волн монохроматического излучения с частотой 600 ТГц укладывается на отрезке 1 м?

1080(1048). Вода освещена красным светом, для которого длина волны в воздухе 0,7 мкм. Какой будет длина волны в воде? Какой цвет видит человек, открывший глаза под водой?

1081(1049). Для данного света длина волны в воде 0,46 мкм. Какова длина волны в воздухе?

1082(1050). Показатель преломления для красного света в стекле (тяжелый флинт) равен 1,6444, а для фиолетового — 1,6852. Найти разницу углов преломления в стекле данного сорта, если угол падения равен 80°.

1083(1051). Какими будут казаться красные буквы, если их рассматривать через зеленое стекло?

1084(1052). Через призму смотрят на большую белую стену. Будет ли эта стена окрашена в цвета спектра?

1085(1053). На черную классную доску наклеили горизонтальную полоску белой бумаги. Как окрасятся верхний и нижний края этой полоски, если на нее смотреть сквозь призму, обращенную преломляющим ребром вверх?

1086(1054). Для получения на экране MN (рис. 120) интерференционной картины поместили источник света S над поверхностью плоского зеркала А на малом расстоянии от него. Объяснить причину возникновения системы когерентных световых волн.

Рис. 120

1087(1055). Две когерентные световые волны приходят в некоторую точку пространства с разностью хода 2,25 мкм. Каков результат интерференции в этой точке, если свет: а) красный (λ = 750 нм); б) зеленый (λ = 500 нм)?

1088(1056). Два когерентных источника S₁ и S₂ освещают экран АВ, плоскость которого параллельна направлению S₁ и S₂ (рис. 121). Доказать, что на экране в точке О, лежащей на перпендикуляре, опущенном на экран из середины отрезка S₁S₂, соединяющего источники, будет максимум освещенности.

Продолжение >>>