Логические функции

Функция, результатом которой является ИСТИНА или ЛОЖЬ, называется логической.

К категории логических относятся функции ЕСЛИ, И, ИЛИ, ИСТИНА, ЛОЖЬ, НЕ.

Функции И, ИЛИ, НЕ позволяют создавать составные логические выражения. Формат этих функций:

И(логическое_значение1; [логическое_значение2]; ...)

ИЛИ(логическое_значение1; [логическое_значение2]; ...)

НЕ(логическоезначение)

Аргументами функций И, ИЛИ, НЕ могут быть логические выражения или ссылки на ячейки, содержащие логические значения.

Функция ЕСЛИ имеет формат:

ЕСЛЩлог выражение; значение_если_истина; значение_если_ложь)

Значение этой функции определяется так:

если лог выражение имеет значение ИСТИНА, то значение функции равно значению выражения значение_если_ истина;
если лог_выражение имеет значение ЛОЖЬ, то значение функции равно значению выражения значение_если_ложь.

Табличные процессоры имеют и такие функции, которые вычисляют сумму, среднее арифметическое, количество не всех значений из диапазонов ячеек, а только тех, которые удовлетворяют определённому условию:

функция СУММЕСЛИ вычисляет сумму тех чисел из указанного диапазона, которые удовлетворяют заданному условию;
функция СРЗНАЧЕСЛИ вычисляет среднее арифметическое тех чисел из указанного диапазона, которые удовлетворяют заданному условию;
функция СЧЁТЕСЛИ подсчитывает количество ячеек из указанного диапазона, содержимое которых удовлетворяет заданному условию.

Пример 1. Пример 1. Выясним, сколько решений имеет логическое уравнение ((х₁ → х₂) → (х₃ → х₄)) = 1.

Преобразуем исходное уравнение, выразив импликацию через инверсию и дизъюнкцию:

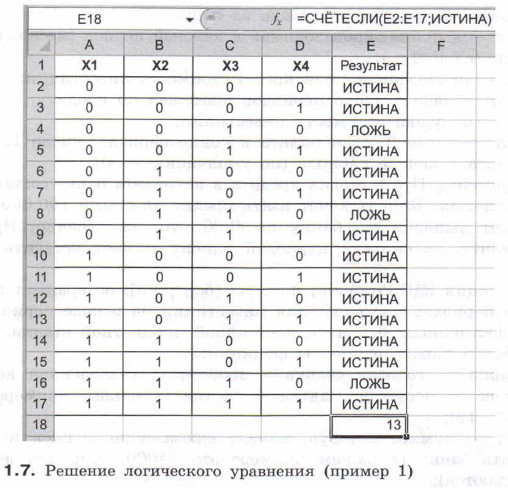
Запишем формулу для вычисления логического выражения с помощью логических функций Microsoft Excel:

=ИЛИ(И(Х1;НЕ(Х2)); НЕ(ХЗ); Х4).

Внесём данные в таблицу и выполним расчёты — рис. 1.7.

Итак, исходное уравнение имеет 13 решений — столько раз встречается значение ИСТИНА в диапазоне Е2:Е17. Для подсчёта этого значения можно воспользоваться функцией СЧЁТЕСЛИ.

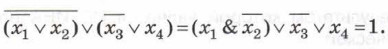
Вспомните другой способ решения этого уравнения.