Отношения между множествами

Отношения могут связывать два множества объектов, например:

«файлы группируются в папки»;
«колеса входят в состав автомобилей»;
«бабочки — это насекомые (являются разновидностью насекомых)».

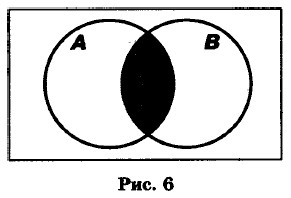
Графически множества удобно представлять с помощью кругов, которые называют кругами Эйлера.

Если множества А и В имеют общие элементы, т. е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются (рис. 6).

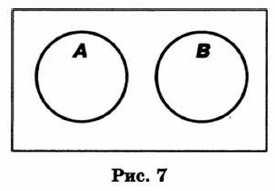
Пример. Пусть А — множество электронных писем, В — множество писем на русском языке. В пересечение этих множеств попадают все электронные письма на русском языке.

Если множества не имеют общих элементов, то говорят, что они не пересекаются (рис. 7).

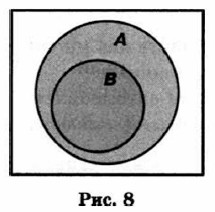
Пример. Пусть А — множество компьютерных устройств ввода информации, В — множество устройств вывода информации. Эти множества не имеют общих элементов.

Если каждый элемент множества В является элементом множества А, то говорят, что В — подмножество А (рис. 8).

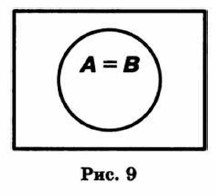
Пример. Пусть А — множество учеников, В — множество шестиклассников. Множество шестиклассников является подмножеством множества учеников.

Если каждый элемент множества В является элементом множества А и, наоборот, каждый элемент множества А является элементом множества В, то говорят, что множества А и В равны (рис. 9).

Пример. Пусть А — множество равносторонних прямоугольников, В — множество квадратов. Эти множества равны.