Главная >> Информатика 9 класс. Босова

§ 1.3. Графические информационные модели

Использование графов при решении задач

Графы удобно использовать при решении некоторых классов задач.

Пример 1. Для того чтобы записать все трёхзначные числа, состоящие из цифр 1 и 2, можно воспользоваться графом (деревом) на рис. 1.7.

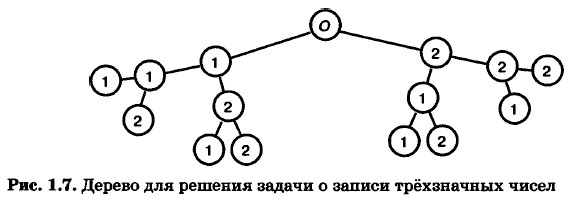
Дерево можно не строить, если не требуется выписывать все возможные варианты, а нужно просто указать их количество. В этом случае рассуждать нужно так: в разряде сотен может быть любая из цифр 1 и 2, в разряде десятков — те же два варианта, в разряде единиц — те же два варианта. Следовательно, число различных вариантов: 2 • 2 • 2 = 8.

В общем случае, если известно количество возможных вариантов выбора на каждом шаге построения графа, то для вычисления общего количества вариантов нужно все эти числа перемножить.

Пример 2. Рассмотрим несколько видоизменённую классическую задачу о переправе.

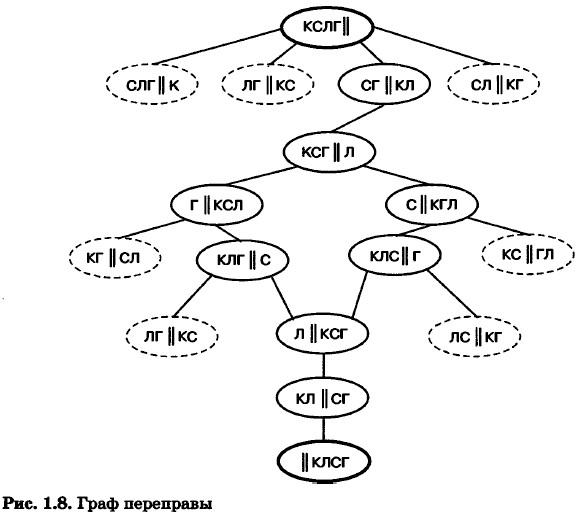
На берегу реки стоит крестьянин (K) с лодкой, а рядом с ним — собака (С), лиса (Л) и гусь (Г). Крестьянин должен переправиться сам и перевезти собаку, лису и гуся на другой берег. Однако в лодку кроме крестьянина помещается либо только собака, либо только лиса, либо только гусь. Оставлять же собаку с лисой или лису с гусем без присмотра крестьянина нельзя — собака представляет опасность для лисы, а лиса — для гуся. Как крестьянин должен организовать переправу?

Для решения этой задачи составим граф, вершинами которого будут исходное размещение персонажей на берегу реки, а также всевозможные промежуточные состояния, достигаемые из предыдущих за один шаг переправы. Каждую вершину-состояние переправы обозначим овалом и свяжем рёбрами с состояниями, образованными из неё (рис. 1.8).

Недопустимые по условию задачи состояния выделены пунктирной линией; они исключаются из дальнейшего рассмотрения. Начальное и конечное состояния переправы выделены жирной линией.

Окончание >>>