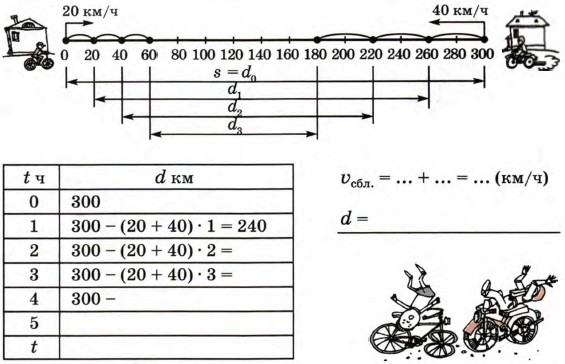
Встречное движение

1. а) Из пунктов А и В, расстояние между которыми равно 300 км, выехали одновременно навстречу друг другу велосипедист и мотоциклист. Скорость велосипедиста 20 км/ч, а скорость мотоциклиста 40 км/ч. Как изменяется расстояние между ними за 1 час? Чему оно будет равно через 1 ч, 2 ч, 3 ч и 4 ч? Когда произойдет встреча? Закончи рисунок, обозначив место встречи флажком. Заполни таблицу и запиши формулу зависимости расстояния d между велосипедистом и мотоциклистом от времени движения t.

б) Придумай, как можно найти время до встречи, не выполняя построений, а лишь с помощью вычислений?

в) Запиши формулу зависимости между величинами: s, υ₁, υ₂ и t_встр., где:

s — первоначальное расстояние;

υ₁ и υ₂ — скорости объектов, движущихся навстречу друг другу;

t_встр. — время до встречи.

2. Два поезда вышли одновременно навстречу друг другу из двух городов, расстояние между которыми 600 км. Скорость первого поезда 70 км/ч, а скорость второго поезда 80 км/ч. Какое расстояние было между поездами через 3 ч после выхода? Через сколько времени после выхода они встретились?

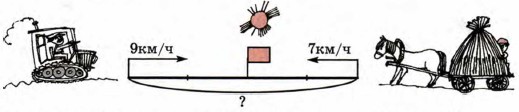
3. Реши задачу двумя способами и определи, какой из способов решения выгоднее? Почему?

Из двух сел выехали одновременно навстречу друг другу трактор и повозка с сеном. Скорость трактора 9 км/ч, а скорость повозки 7 км/ч. Чему равно расстояние между селами, если встреча произошла через 2 ч после начала движения?

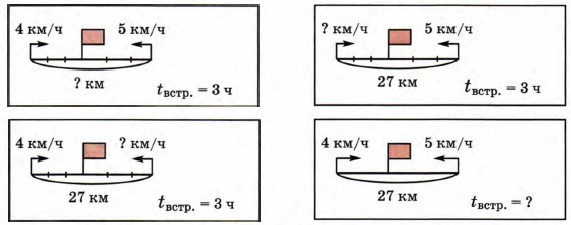
4. Составь по схемам задачи и реши их. Что ты замечаешь?

5. Бассейн вмещает 300 м³ воды и наполняется двумя трубами. Через первую трубу вода вливается со скоростью 20 м³/ч, а через вторую трубу — со скоростью 30 м³/ч. За сколько времени наполнится пустой бассейн при одновременном включении двух труб? Сколько кубических метров воды вольется в бассейн за 4 ч? Какой объем при этом останется незаполненным?

Окончание >>>