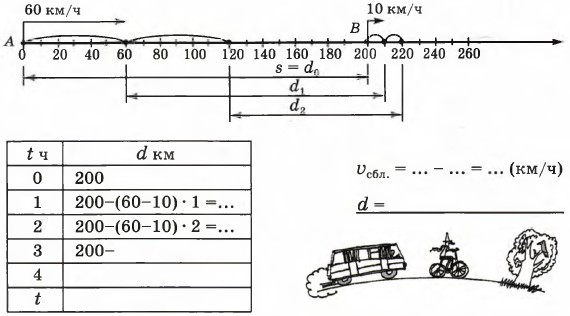
Движение вдогонку

1. а) Из пунктов А и В, удаленных друг от друга на 200 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 10 км/ч, а автобус догоняет его со скоростью 60 км/ч. Как изменяется расстояние между ними за 1 час? Чему оно будет равно через 1 ч, 2 ч, 3 ч, t ч? Когда произойдет встреча?

Закончи построения на координатном луче и обозначь место встречи флажком. Заполни таблицу и запиши формулу зависимости расстояния d между автобусом и велосипедистом от времени движения t.

б) Как найти время до встречи с помощью вычислений? Докажи.

в) Запиши формулу зависимости между величинами s, υ1, υ2 и t_встр., где:

S — первоначальное расстояние;

υ₁ и υ₂ — скорости объектов, движущихся вдогонку (υ₁ > υ₂);

t_встр. — время до встречи.

2. Миша начал догонять Борю, когда расстояние между ними было 100 м. Миша идет со скоростью 80 м/мин, а Боря — со скоростью 60 м/мин. Через сколько времени Миша догонит Борю?

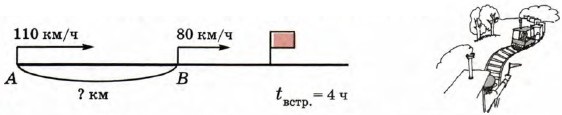
3. Из пунктов А и В одновременно в одном направлении выехали 2 поезда. Скорость первого поезда равна 80 км/ч, а скорость второго поезда, идущего вдогонку первому поезду, равна 110 км/ч. Встреча произошла через 4 ч после выезда поездов. На каком расстоянии друг от друга находятся пункты А и В?

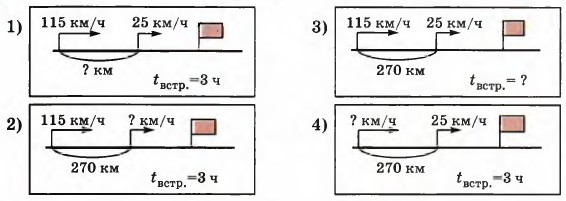
4. Составь по схемам задачи и реши их. Что ты замечаешь?

5. Придумай задачу на движение вдогонку, в которой надо узнать: а) время до встречи; б) скорость одного из движущихся объектов; в) первоначальное расстояние между ними.

6. В бочку с водой проведен шланг, через который в нее вливается 9 ведер воды в час. Через другой шланг водой из бочки поливают огород, расходуя при этом 16 ведер воды в час. Через сколько времени опустошится полная бочка, вмещающая 21 ведро воды, если оба шланга начнут использоваться одновременно?

Окончание >>>