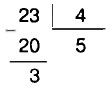|
|
|
|
|
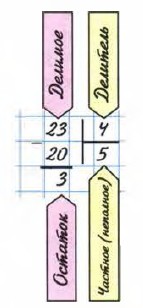
§ 3. Умножение и деление натуральных чисел 13. Деление с остаткомДеление одного натурального числа на другое нацело не всегда возможно. Пусть, например, бабушка даст 23 конфеты 4 внукам и предложит разделить их поровну. Тогда каждому внуку достанется 5 конфет и 3 конфеты останутся. Получается деление с остатком числа 23 на 4:
Число 23 здесь делимое, 4 — делитель, 5 — неполное частное и 3 — остаток.
В числе 23 содержится 5 раз по 4 да ещё 3. Имеем: 23 = 4 • 5 + 3.
Чтобы найти делимое при делении с остатком, надо умножить неполное частное на делитель и к полученному произведению прибавить остаток.
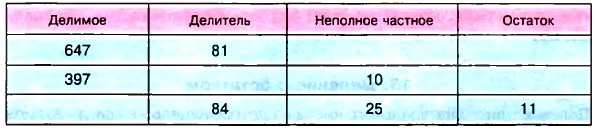
529. Масса чугунной болванки 20 кг. Сколько деталей по 18 кг можно отлить из 10 болванок? Сколько чугуна останется? 530. На пошив одного пододеяльника требуется 6 м полотна. Сколько пододеяльников можно сшить из 200 м полотна? Сколько полотна останется? 531. Масса чугунной болванки 16 кг. Сколько таких болванок потребуется для отливки 41 детали, каждая из которых имеет массу 12 кг? Сколько чугуна останется? 532. Заполните таблицу:
533. Выполните деление с остатком:
534. Какие остатки могут получиться при делении различных чисел на 2; на 7; на 10; на 23; на 200?
|
|
|