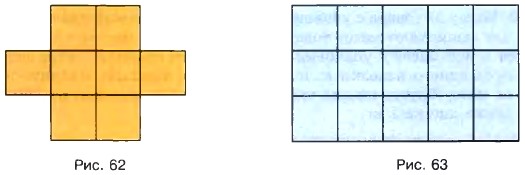
18. Площадь. Формула площади прямоугольника

Фигура на рисунке 62 состоит из 8 квадратов со стороной 1 см каждый. Площадь одного такого квадрата называют сантиметром. Пишут: 1 см². Значит, площадь всей фигуры равна 8 см².

Если какую-нибудь фигуру можно разбить на р квадратов со стороной 1 см, то её площадь равна р см².

Прямоугольник на рисунке 63 состоит из 3 полос, каждая из которых разбита на 5 квадратов со стороной 1 см. Весь прямоугольник состоит из 5 • 3 = 15 таких квадратов, и его площадь равна 15 см².

Чтобы найти площадь прямоугольника, надо умножить его длину на ширину.

Запишем это правило в виде формулы. Площадь прямоугольника обозначим буквой S, его длину — буквой а, а ширину — буквой b.
Получаем формулу площади прямоугольника:
S = ab.

Две фигуры называют равными, если одну из них можно так наложить на вторую, что эти фигуры совпадут.

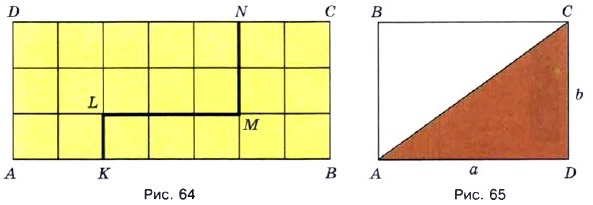
Площади равных фигур равны. Их периметры тоже равны.

Линия KLMN на рисунке 64 разбивает прямоугольник ABCD на две части. Одна из частей имеет площадь 12 см², а другая — 9 см². Площадь всего прямоугольника равна 3 • 7, то есть 21 см². При этом 21 = 12 + 9.

Площадь всей фигуры равна сумме площадей её частей.

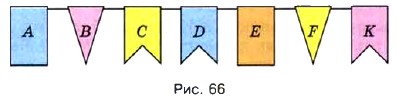
Отрезок АС разбивает прямоугольник на два равных треугольника: АВС и ADC (рис. 65).

Площадь каждого треугольника равна половине площади всего прямоугольника.

Квадрат — это прямоугольник с равными сторонами.

Если сторона квадрата равна 4 см, то его площадь равна 4 • 4, то есть 42 см² = 16 см².

Если сторона квадрата равна о, то площадь S квадрата равна а • а = а².
Значит, формула площади квадрата имеет вид
S = а².

Именно поэтому запись а² называют квадратом числа а.

709. Какие из флажков на рисунке 66 равны?

710. Равны ли друг другу листы одной тетради? Почему?

711. Равны ли выкройка и вырезанный по ней кусок материи?

Продолжение >>>