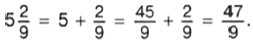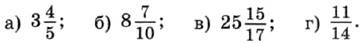|
|
|
|
|
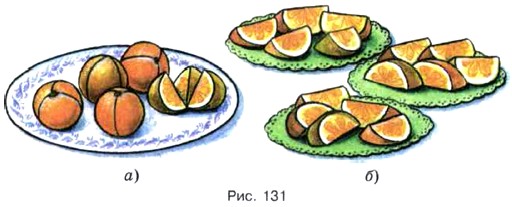
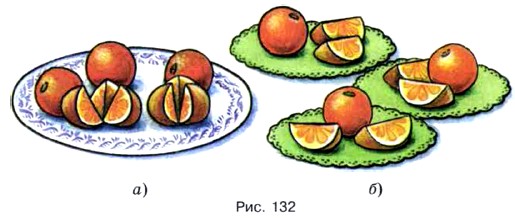
§ 5. Обыкновенные дроби 28. Смешанные числаРазделить поровну 5 одинаковых апельсинов между тремя детьми можно двумя способами. Во-первых, можно разделить между ними поровну каждый апельсин (рис. 131, а). Тогда один ребёнок получит по 5 частей, а каждая из этих частей равна Во-вторых, можно сначала дать каждому из детей по целому апельсину, а оставшиеся 2 апельсина разделить между ними поровну (рис. 132, а). Тогда каждый из детей получит
Сумму Так как в обоих случаях каждый ребёнок получает одно и то же количество апельсинов, то числа
Чтобы перейти от записи
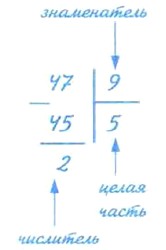
Чтобы из неправильной дроби выделить целую часть, надо:
Пример 1. Выделим целую часть из неправильной дроби Р е ш е н и е. Делим 47 на 9. Неполное частное равно 5, а остаток равен 2. Значит,
Запись числа, содержащую целую и дробную части, называют смешанной. Для краткости вместо «число в смешанной записи» говорят смешанное число. Смешанное число можно представить и в виде неправильной дроби. Пример 2. Представим в виде неправильной дроби число Р е ш е н и е. Мы знаем, что
Чтобы представить смешанное число в виде неправильной дроби,
1084. Представьте число в виде суммы его целой и дробной частей:
|
|
|



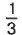 целого апельсина (рис. 131, б). Поэтому каждый ребёнок получит
целого апельсина (рис. 131, б). Поэтому каждый ребёнок получит 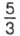 апельсина.
апельсина.
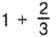 апельсина (рис. 132, б).
апельсина (рис. 132, б).

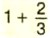 принято записывать короче:
принято записывать короче: 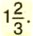 Запись
Запись 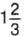 читают так: «Одна целая две третьих».
читают так: «Одна целая две третьих».
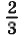 — его дробной частью.
— его дробной частью.
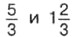 равны:
равны: 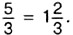


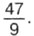
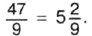
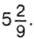
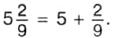 Но 5 можно записать в виде дроби со знаменателем 9, а именно:
Но 5 можно записать в виде дроби со знаменателем 9, а именно: 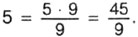 Значит,
Значит,