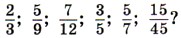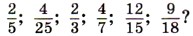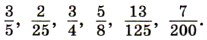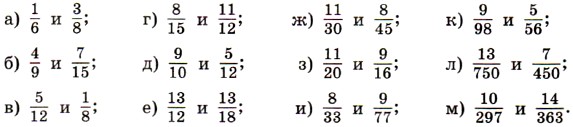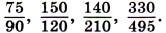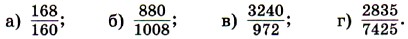|
|
|
|
|
§2. Сложение и вычитание дробей с разными знаменателями 10. Приведение дробей к общему знаменателю (продолжение)Итак, К какому новому знаменателю можно привести данную дробь?
275. Приведите дробь:
276. Выразите в минутах, а потом в шестидесятых долях часа:
277. Сколько содержится:
278. Сократите дроби 279. Можно ли привести к знаменателю 36 дроби:
280. Можно ли представить в виде десятичной дроби:
В каком случае обыкновенную дробь можно представить в виде десятичной? 281. Запишите в виде десятичной дроби, приведя:
282. Запишите в виде десятичной дроби:
283. Приведите к наименьшему общему знаменателю дроби:
284. Вычислите устно:
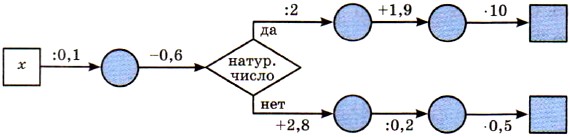
285. Найдите пропущенные числа, если х = 0,8; 0,16; 0,06; 1:
286. На какое число надо умножить 24 ; 8 ; 1 6 ; 6 ; 12 , чтобы получить 48?
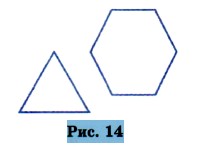
287. С помощью транспортира разделите одну окружность на 6, а другую — на 3 равные дуги. Постройте многоугольники, изображённые на рисунке 14. У каждого из этих многоугольников равны стороны и равны углы. Такие многоугольники называют правильными. Подумайте, является ли правильным многоугольником прямоугольник; квадрат. 288. Сократите: 289. Найдите наибольший общий делитель числителя и знаменателя и сократите дробь:
|
|
|




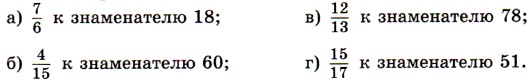
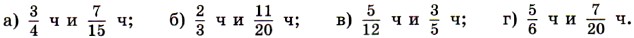
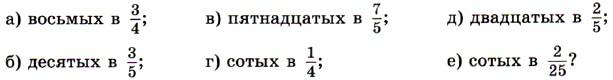
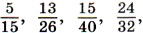 , а потом приведите их к знаменателю 24.
, а потом приведите их к знаменателю 24.