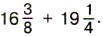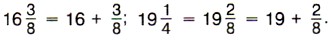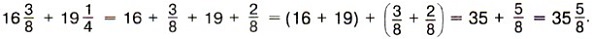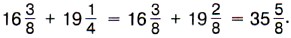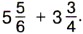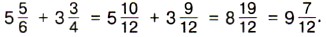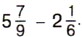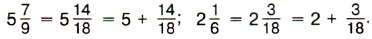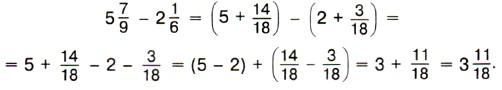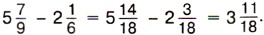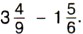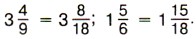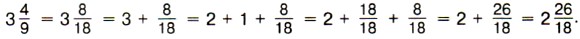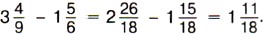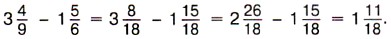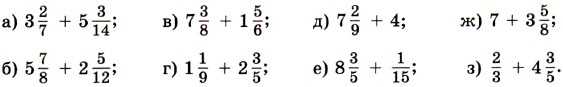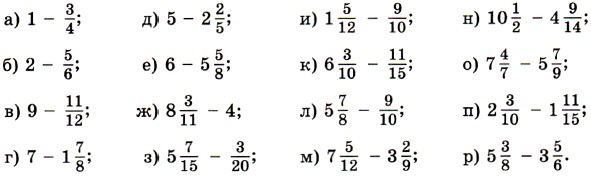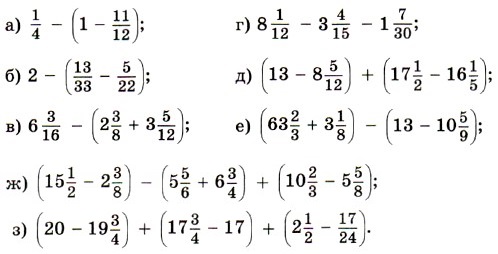|
|
|
|
|
§ 2. Сложение и вычитание дробей с разными знаменателями 12. Сложение и вычитание смешанных чиселПереместительное и сочетательное свойства сложения позволяют привести сложение смешанных чисел к сложению их целых частей и к сложению их дробных частей. Пример 1. Найдём значение суммы Р е ш е н и е. Приведём дробные части чисел к наименьшему общему знаменателю 8, затем представим смешанные числа в виде суммы их целой и дробной частей:
Значит,
Пишут короче: Пример 2. Найдём значение суммы Р е ш е н и е. Сначала приводим дробные части данных чисел к наименьшему общему знаменателю 12, затем отдельно складываем целые и дробные части:
При вычитании смешанных чисел пользуются свойствами вычитания суммы из числа и вычитания числа из суммы. Пример 3. Найдём значение разности Р е ш е н и е. Приведём дробные части к наименьшему общему знаменателю 18 и представим данные числа в виде суммы целой и дробной частей:
По свойству вычитания суммы из числа имеем:
Пишут короче: Если дробная часть уменьшаемого окажется меньше дробной части вычитаемого, то надо превратить в дробь с тем же знаменателем одну единицу целой части уменьшаемого. Пример 4. Найдём значение разности Р е ш е н и е. Приведём дробные части данных чисел к наименьшему общему знаменателю 18:
Так как дробная часть уменьшаемого меньше дробной части вычитаемого, то уменьшаемое записываем так:
Значит, Обычно пишут короче:
Расскажите, как сложить смешанные числа и на каких свойствах сложения основано сложение смешанных чисел.
376. Выполните сложение:
377. Выполните вычитание:
378. Найдите значение выражения:
|
|
|