|
|
|
|
|
§ 3. Умножение и деление обыкновенных дробей 13. Умножение дробейЗадача 1. В бутылке Р е ш е н и е . Для решения задачи надо найти произведение
Значит, в 5 бутылках
Задача 2. Длина прямоугольника Р е ш е н и е. Из рисунка видно, что данный прямоугольник можно получить так: разделить одну сторону квадрата со стороной 1 дм на 5 одинаковых частей и взять 4 такие части, а другую сторону разделить на 3 одинаковые части и взять 2 такие части. При таком делении квадрат будет состоять из 15 равных частей, а прямоугольник будет состоять из 8 таких частей. Значит, площадь прямоугольника равна Итак,
Обычно вначале обозначают произведение числителей и произведение знаменателей, затем производят сокращение и только потом выполняют умножение. В ответе, если это возможно, из дроби исключают целую часть. Например:
Задача 3. Сколько километров проедет велосипедист за Р е ш е н и е. Так как пройденный путь равен произведению скорости и времени, то для решения задачи надо найти произведение чисел Представим каждое из этих чисел в виде неправильной дроби:
Теперь воспользуемся правилом умножения дробей. Получим:
Таким образом, за
С помощью умножения дробей решают такие же задачи, как и с помощью умножения натуральных чисел. Задача 4. За 1 ч автоматическая линия производит Р е ш е н и е. Такие задачи с натуральными числами или с десятичными дробями мы решали с помощью умножения. Решим и эту задачу умножением:
Итак, за Тот же ответ можно получить, если выразить данные числа в десятичных дробях:
Умножение дробей обладает переместительным и сочетательным свойствами. Кроме того, для любого значения а:
Например, Расскажите, как умножить дробь на натуральное число.
427. Выполните умножение:
428. Сторона квадрата 429. В одну банку помещается 430. Найдите периметр треугольника АБС, если АВ =
|
|
|



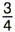 сока. Сколько сока в 5 таких бутылках?
сока. Сколько сока в 5 таких бутылках?
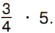 Но умножить
Но умножить 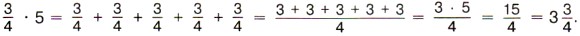
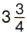 л сока.
л сока.
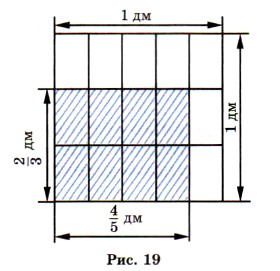
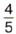 дм, а ширина
дм, а ширина 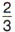 дм (рис. 19). Чему равна площадь прямоугольника?
дм (рис. 19). Чему равна площадь прямоугольника?
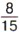 дм2. Но мы знаем, что площадь прямоугольника равна произведению длины и ширины. Следовательно, число
дм2. Но мы знаем, что площадь прямоугольника равна произведению длины и ширины. Следовательно, число 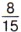 можно получить умножением
можно получить умножением 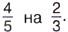
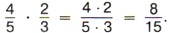
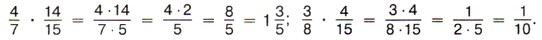
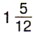 ч, если будет двигаться со скоростью
ч, если будет двигаться со скоростью 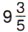 км/ч?
км/ч?
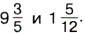
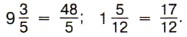
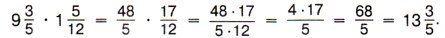
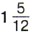 велосипедист проедет
велосипедист проедет 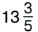 км.
км.
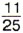 ц пластмассы. Сколько пластмассы линия производит за
ц пластмассы. Сколько пластмассы линия производит за 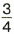 ч?
ч?
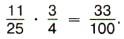
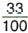 ц пластмассы, т. е. 33 кг.
ц пластмассы, т. е. 33 кг.
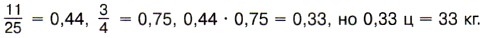
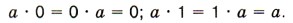
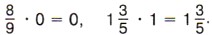

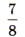 м. Найдите периметр квадрата.
м. Найдите периметр квадрата.
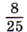 кг крупы. Сколько этой крупы вместят две, пять, десять таких же банок?
кг крупы. Сколько этой крупы вместят две, пять, десять таких же банок?
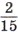 , ВС больше АВ в 4 раза, а АС меньше ВС на
, ВС больше АВ в 4 раза, а АС меньше ВС на 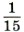 м.
м.