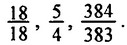|
|
|
|
|
2. Признаки делимости на 10, на 5 и на 2 Признаки делимости на 10, на 5 и на 2": Ответы (окончание)47. а) Двузначные делители числа 100: 10, 20,25, 50; б) двузначные числа, кратные 25: 25, 50, 75; в) 25, 50. 48. Если b делитель числа а, а можно представить в виде произведения а = b • r, где r - частное. Видно, что число r тоже будет делителем числа а. 18 = 3 • 6; 6 также является делителем числа 18. 49. а) Если а кратно b,a b кратно с, а = n • b , b = m • c; a = n • b = n • (m • c = (n-m) n • m — натуральное число, значит a кратно с; б) а = n • 6, b=m • 6, а + b = n • б + m • 6=(n + m) • 6, т. е. а + b делится на 6. 50. Правильные дроби: 51. При а = 4, 5, 6, 7, 8, 9, 10 дробь 52. а)(x + 2,3) • 0.2 = 0,7; x + 2,3 = 0,7 : 0.2; x + 2,3 = 3,5; x = 1,2;
53. а) 6! = 1 • 2 • 3 • 4 • 5 • 6 = 72 (72) способами; б) 2 • 5! = 24 (24) способами 54. 1) Число до уменьшения на 2,75 было равно: 85,25 + 2,75 - 88; задуманное число равно: 88 : 11 = 8; 2) Число до увеличения в 11 раз было равно: 110 : 11 = 10; задуманное число равно: 10 - 9,2 = 0,8. 55. а) 154,174,178, 320, 346; б) 315, 320, 425,475; в) 320; г) 161, 191,315,425,475. 56. а) 12, 14, 16, 18,20; б) 13, 17, 19, 21. 57 . 1000, 1005, 5000. 58. Правильные дроби: 59. а) (4,9 - х) : 1,2 = 3; 4,9 - x = 31,2; 4,9 - x = 3,6; x = 4,9 - 3,6; x = 1,3; б) 3,8 • (x - 0,2) = 2,28; x - 0,2 = 2,28 : 3,8; x - 0,2 = 0,6; x = 0,6 + 0,2; x = 0,8 60. а) (93 • 7 + 141 ) : 72 = (651+141 ) : 72 = 792 : 72 = 11;
|
|
|



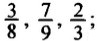 неправильные дроби:
неправильные дроби: 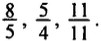
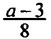 будет правильной; при b = 1, 2, 3, 4, 5, 6, 7 дробь
будет правильной; при b = 1, 2, 3, 4, 5, 6, 7 дробь 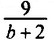 будет неправильной.
будет неправильной.
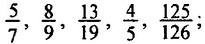 неправильные дроби
неправильные дроби