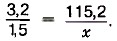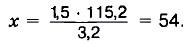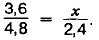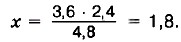|
|
|
|
|
§ 4. Отношения и пропорции 22. Прямая и обратная пропорциональные зависимостиЕсли станок с числовым программным управлением за 2 ч изготовляет 28 деталей, то за вдвое большее время, т. е. за 4 ч, он изготовит вдвое больше таких деталей, т. е. 28 • 2 = 56 деталей. Во сколько раз больше времени будет работать станок, во столько раз больше деталей он изготовит. Значит, равны отношения 4 : 2 и 56 : 28. Следовательно, верна пропорция 4 : 2 = 56 : 28. Такие величины, как время работы станка и число изготовленных деталей, называют прямо пропорциональными величинами.
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны. Пусть путь из города А в город В поезд со скоростью 40 км/ч проходит за 12 ч. Если скорость движения увеличить вдвое, т. е. сделать её равной 80 км/ч, то на этот же путь поезд затратит вдвое меньше времени, т. е. 6 ч. Во сколько раз увеличится скорость движения, во столько же раз уменьшится время движения. В этом случае отношение 80 : 40 будет равно не отношению 6:12, а обратному отношению 12:6. Следовательно, верна пропорция 80 : 40 = 12 : 6. Такие величины, как скорость и время, называют обратно пропорциональными величинами.
Если величины обратно пропорциональны, то отношение значений одной величины равно обратному отношению соответствующих значений другой величины. Не всякие две величины являются прямо пропорциональными или обратно пропорциональными. Например, рост ребёнка увеличивается при увеличении его возраста, но эти величины не являются пропорциональными, так как при удвоении возраста рост ребёнка не удваивается. Задачи на пропорциональные величины можно решить с помощью пропорции. Задача 1. За 3,2 кг товара заплатили 115,2 р. Сколько следует заплатить за 1,5 кг этого товара? Р е ш е н и е. Запишем кратко условие задачи в виде таблицы, обозначив буквой х стоимость (в рублях) 1,5 кг этого товара. Запись будет иметь следующий вид:
Зависимость между количеством товара и стоимостью покупки прямо пропорциональна, так как если купить товара в несколько раз больше, то и стоимость покупки увеличится во столько же раз. Условно обозначим такую зависимость одинаково направленными стрелками. Запишем пропорцию:
Теперь найдём неизвестный член пропорции:
Ответ: 54 р. Задача 2. Два прямоугольника имеют одинаковую площадь. Длина первого прямоугольника 3,6 м, а ширина 2,4 м. Длина второго прямоугольника 4,8 м. Найдите ширину второго прямоугольника. Р е ш е н и е. Обозначив буквой х ширину (в метрах) второго прямоугольника, запишем кратко условие задачи:
Зависимость между шириной и длиной при одном и том же значении площади прямоугольника обратно пропорциональная, так как если увеличить длину прямоугольника в несколько раз, то надо ширину во столько же раз уменьшить. Условно обозначим такую зависимость противоположно направленными стрелками. Запишем пропорцию:
Теперь найдём неизвестный член пропорции:
Ответ: 1,8 м.
|
|
|