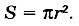|
|
|
|
|
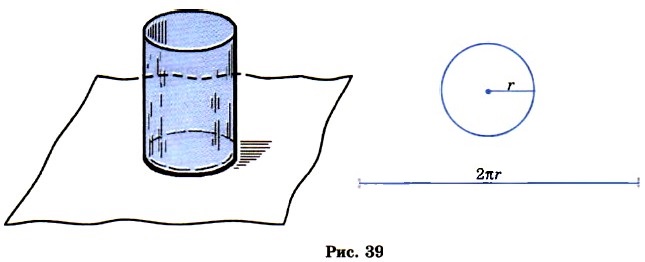
§ 4. Отношения и пропорции 24. Длина окружности и площадь кругаВозьмём круглый стакан, поставим на лист бумаги и обведём его карандашом. На бумаге получится окружность. Если «опоясать» стакан ниткой, а потом распрямить её, то длина нитки будет приближённо равна длине нарисованной окружности (рис. 39).
Длина окружности прямо пропорциональна длине её диаметра. Поэтому для всех окружностей отношение длины окружности к длине её диаметра является одним и тем же числом. Его обозначают греческой буквой Так как диаметр окружности вдвое больше её радиуса, то длина окружности с радиусом г равна 2 Получили другую формулу длины окружности: С = 2 Подсчёты показали, что с точностью до десятитысячных
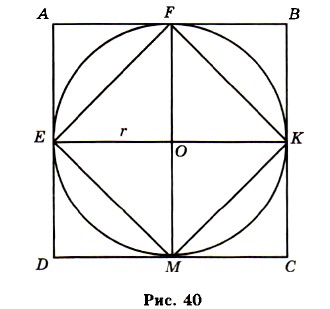
На рисунке 40 изображены круг и два квадрата ABCD и EFKM. Радиус круга равен г, поэтому длина стороны квадрата ABCD равна 2r, а его площадь 4r2. Площадь треугольника EOF вдвое меньше площади квадрата AEOF, поэтому площадь EFKM вдвое меньше площади квадрата ABCD, т. е. равна 2r2. Площадь круга S больше площади квадрата EFKM, но меньше площади квадрата ABCD: 2r2 < S < 4r2. Примерно площадь круга равна 3r2. Можно доказать, что
Напишите формулы для нахождения длины окружности по длине её диаметра и по длине её радиуса.
847. Найдите длину окружности, радиус которой равен 24 см; 4,7 дм; 18,5 м. Число
|
|
|



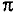 (читается: «пи»). Если обозначить длину окружности буквой С, а длину диаметра буквой d, то С : d =
(читается: «пи»). Если обозначить длину окружности буквой С, а длину диаметра буквой d, то С : d = 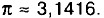 Если значение округлить до сотых, то получим значение 3,14. Примерно такую же точность даёт значение
Если значение округлить до сотых, то получим значение 3,14. Примерно такую же точность даёт значение 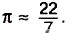 В старших классах будет рассказано, как проводились такие подсчёты.
В старших классах будет рассказано, как проводились такие подсчёты.