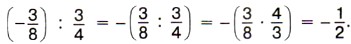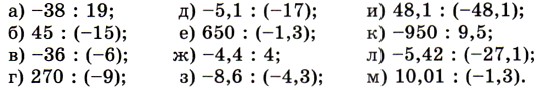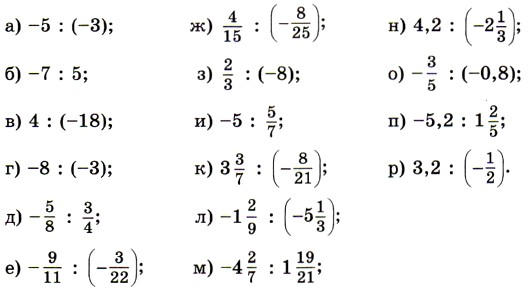|
|
|
|
|
§ 7. Умножение и деление положительных и отрицательных чисел 36. ДелениеДеление отрицательных чисел имеет тот же смысл, что и деление положительных чисел: по данному произведению и одному из множителей находят второй множитель. Например, разделить -12 на -4 — это значит найти такое число х, что -4-х = -12. Сначала найдём знак числа х. Так как при умножении -4 на х получилось отрицательное число -12, то множители -4 и x должны иметь разные знаки. Поэтому х — положительное число. Теперь найдём модуль числа х. Так как модуль произведения равен произведению модулей множителей, то |—12| = |—4| • |х|. Отсюда |х| = |—12| : |—4|. Но так как х — положительное число, то х = |х|. Значит, х = 3. Пишут: (-12) : (-4) = |—12| : |—4| = 3, или короче: (-12) : (-4) = 12:4 = 3.
Например, -4,5 : (-1,5) = 4,5 : 1,5 = 3; Разделить -24 на 4 — это значит найти такое число х, что 4-х = -24. При умножении 4 на х получилось отрицательное число -24, значит, множители 4 и х должны иметь разные знаки. Поэтому х — отрицательное число. При этом должно выполняться равенство |4|•|х| = |—24|. Отсюда |х| = |—24| : |4| = 24 : 4 = 6. Значит, х — отрицательное число с модулем 6, т. е. х = -6. Итак, -24 : 4 = -6. Рассуждая таким же образом, получим, что 24 : (-4) = -6.
Обычно вначале определяют и записывают знак частного, а потом уже находят модуль частного. Например, 3,6 : (-3) = -(3,6 : 3) = -1,2;
При делении нуля на любое число, не равное нулю, получается нуль. Делить на нуль нельзя! Сформулируйте правило деления отрицательного числа на отрицательное. 1149. Верно ли выполнено деление:
1150. Найдите частное:
1151. Выполните деление:
|
|
|