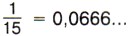|
|
|
|
|
§ 7. Умножение и деление положительных и отрицательных чисел 37. Рациональные числа
Любое целое число а является рациональным числом, так как его можно a
записать в виде Например, Рациональным числом будет и любая отрицательная дробь, так как, например, Числа Сумма, разность и произведение рациональных чисел тоже рациональные числа. Например:
Если делитель отличен от нуля, то частное двух рациональных чисел тоже рациональное число. Например:
Вы уже умеете выражать некоторые обыкновенные дроби в виде десятичных дробей. Например,
Не все обыкновенные дроби можно представить в виде десятичной дроби. Например, если будем делить 1 на 3, то получим сначала нуль целых, потом три десятых, а далее при делении всё время будут повторяться остаток 1 и в частном цифра 3. Деление никогда не кончится. Значит, дробь Разделив 5 на 11, получим, что В записях 0,333..., 0,4545... и 0,0666... одна или несколько цифр начинают повторяться бесконечно много раз. Такие записи называют периодическими дробями. Вместо 0,333... пишут 0,(3), вместо 0,4545... пишут 0,(45), а вместо 0,0666... пишут 0,0(6). Любое рациональное число можно записать либо в виде десятичной дроби (в частности, целого числа), либо в виде периодической дроби.
|
|
|



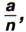 где а — целое число, а n — натуральное число, называют рациональным числом.
где а — целое число, а n — натуральное число, называют рациональным числом.
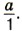
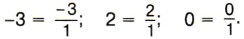
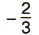 можно записать так:
можно записать так: 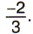
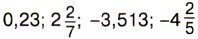 тоже рациональные числа, так как
тоже рациональные числа, так как 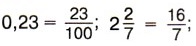
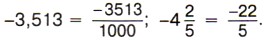
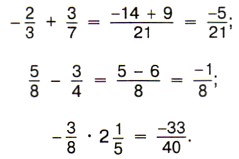
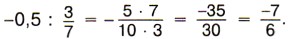


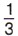 нельзя представить в виде десятичной дроби. Но если разрешить писать бесконечные десятичные дроби, то
нельзя представить в виде десятичной дроби. Но если разрешить писать бесконечные десятичные дроби, то 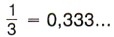
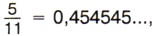 а разделив 1 на 15, получим, что
а разделив 1 на 15, получим, что