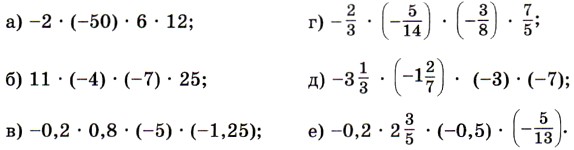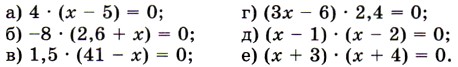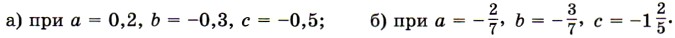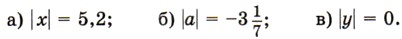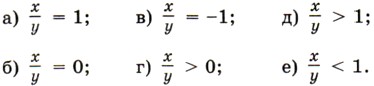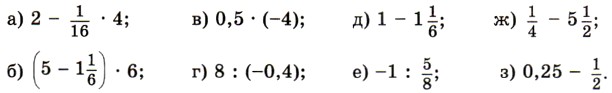|
|
|
|
|
§ 7. Умножение и деление положительных и отрицательных чисел 38. Свойства действий с рациональными числами (продолжение)1208. Сформулируйте словами сочетательное свойство умножения а(bс) = (ab)c и проверьте его:
1209. Выбирая удобный порядок вычислений, найдите значение выражения:
1210. Какое получится число (положительное или отрицательное), если перемножить: а) одно отрицательное и два положительных числа;
1211. Определите знак произведения: а) -2 • (-3) • (-9) • (-1,3) • 14 • (-2,7) • (-2,9);
1212. Решите уравнение, использовав свойство произведения, равного нулю:
1213. Сформулируйте словами распределительное свойство умножения (а + b) • с = ас + bс и проверьте его:
1214. Выбирая удобный порядок вычислений, найдите значение выражения:
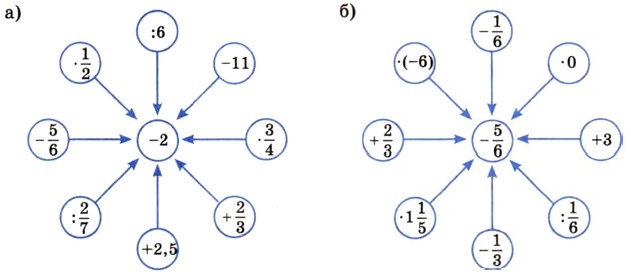
1215. Вычислите устно:
1216. Найдите сумму всех целых чисел: а) от -6 до 7; б) от -18 до 17; в) от -22 до 20. 1217. Решите уравнение:
1218. Придумайте такие значения х и у, при которых верно соотношение:
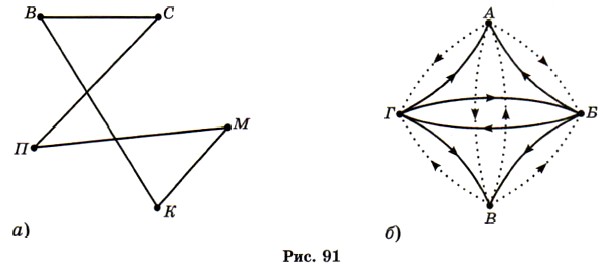
1219. Найдите наибольшее значение выражения: а) -|x|; б) 2 - |х|; в) -|х - 1|; г) -(х - 1)2. 1220. Решать некоторые математические задачи помогают специальные схемы, состоящие из точек и соединяющих их дуг или стрелок рис. 91). Такие схемы называют графами, точки называют вершйнами графа, а дуги — рёбрами графа. Ответьте на вопросы, используя графы. а) В спортивном зале собрались Витя, Коля, Петя, Серёжа и Максим (рис. 91, а). Оказалось, что каждый из мальчиков знаком только с двумя другими. Кто с кем знаком? (Ребро графа означает «мы знакомы».) б) Во дворе гуляют братья и сёстры одной семьи. Кто из этих детей мальчики, а кто девочки (рис. 91,б)? (Пунктирные рёбра графа исходят от сестёр, а сплошные — от братьев.)
1221. Вычислите:
|
|
|