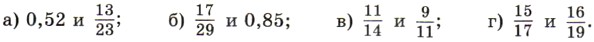|
|
|
|
|
§ 9. Координаты на плоскости 48. Вопросы и задачи на повторение1469. Приведите примеры: а) целых чисел; б) натуральных чисел; в) отрицательных чисел, не являющихся целыми; г) положительных чисел, не являющихся натуральными; д) рациональных чисел, не являющихся целыми; е) двух рациональных взаимно обратных чисел; ж) двух противоположных целых чисел; з) двух рациональных чисел, произведение которых равно 0; равно 1; и) двух целых чисел, сумма которых равна 0; равна 1. 1470. При каком условии равно нулю: а) произведение рациональных чисел;
1471. Верно ли, что: а) число, обратное произведению двух чисел, равно произведению чисел, обратных множителям; б) число, обратное сумме двух чисел, равно сумме чисел, обратных слагаемым; в) число, противоположное произведению двух чисел, равно произведению чисел, противоположных множителям; г) число, противоположное сумме двух чисел, равно сумме чисел, противоположных слагаемым? 1472. Найдите значение выражения:
1473. Ответьте на вопросы. а) Какое число называют делителем данного числа? кратным данного числа? Приведите примеры.
1474. Сформулируйте основное свойство дроби. Приведите примеры использования основного свойства дроби. 1475. Из натуральных чисел, расположенных между числами 11 и 43, выпишите те числа, которые: а) кратны числу 7; б) кратны числу 3; в) кратны числу 9; г) кратны числу 5; д) нечётные. 1476. Запишите все делители чисел 18; 24; 45. 1477. Какие из чисел 3572, 81 375, 158 457, 237 583, 67 932, 2 487 960 делятся нацело на 3? делятся нацело на 9? делятся нацело на 5? делятся нацело на 15? 1478. Найдите значение выражения:
1479. Верно ли, что: а) сумма простых чисел есть число простое;
480. При строительстве железной дороги перемещается грунт. Сколько ездок должен сделать 25-тонный грузовик, чтобы перевезти 220 млн м3 грунта, если масса одного кубометра грунта 1481. Сформулируйте и запишите с помощью букв: а) свойства сложения рациональных чисел; б) свойства умножения рациональных чисел; в) свойства нуля при сложении; г) свойства 0 и 1 при умножении рациональных чисел. Придумайте примеры, в которых использование свойств арифметических действий упрощает вычисления. 1482. Постройте столбчатую диаграмму сравнительной продолжительности жизни некоторых деревьев по следующим данным: баобаб — 5000 лет, кипарис — 3000 лет, кедр — 1200 лет, дуб — 1000 лет, сосна обыкновенная — 600 лет, берёза — 250 лет, рябина — 80 лет. 1483. Ответьте на вопросы. а) Чему равен модуль положительного числа; отрицательного числа? Чему равен модуль нуля?
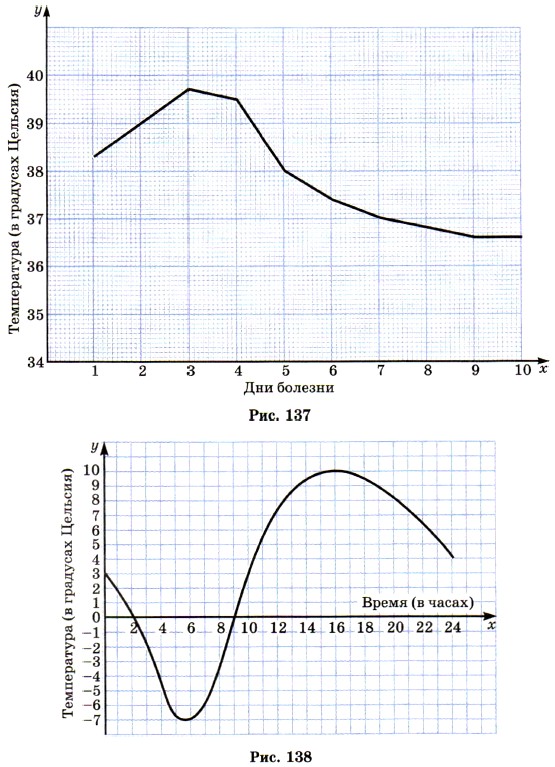
1484. Валерий заболел. На рисунке 137 показано изменение температуры больного. Ответьте на вопросы. а) Сколько дней у Валерия была повышенная температура?
1485. На рисунке 138 изображён график изменения температуры воздуха в течение суток. Определите по графику: а) температуру воздуха в 4 ч; в 14 ч; в 22 ч;
1486. По какому правилу выполняется: а) сложение дробей с одина ковыми знаменателями; б) сложение дробей с разными знаменателями в) умножение дробей; г) деление дробей; д) сравнение рациональных чисел; е) сложение рациональных чисел с одинаковыми знаками; с разными знаками; ж) вычитание рациональных чисел; з) умножение рациональных чисел с одинаковыми знаками; с разными знаками; и) деление рациональных чисел с одинаковыми знаками; с разными знаками; к) раскрытие скобок, перед которыми стоит знак «+»; знак «-»? 1487. В каком порядке следует выполнять действия в выражении без скобок, если в нём содержится по одному разу вычитание, возведение числа в куб и деление? 1488. Выполните действия:
1489. Найдите значение выражения:
1490. Составьте программу вычислений и с помощью микрокалькулятора найдите значение выражения:
1491. Сравните числа с помощью вычитания:
1492. Узнайте:
1493. Здание Кремлёвского дворца съездов в Москве имеет форму прямоугольного параллелепипеда длиной 120 м и общим объёмом 369 600 м3. Найдите высоту здания над землёй, если оно заглублено в землю на 15 м и длина здания больше его ширины в 1494. Выполните действия:
1495. Приведите примеры: а) отношения двух величин;
1496. В чём состоит основное свойство пропорции? Придумайте примеры использования этого свойства пропорции: а) для доказательства, что пропорция верна;
1497. а) Чему равно отношение длины окружности к её диаметру? отношение площади круга к квадрату его радиуса? б) По какой формуле вычисляется длина окружности? площадь круга?
1498. Сравните числа, найдя их отношение:
1499. Бригада проходчиков при строительстве тоннеля метро в течение недели ежедневно проходила по 0,8 м. За х дней длина тоннеля увеличилась на у метров. Выразите у через х. Является ли зависимость у от х прямой пропорциональностью? Найдите значение у при х = 1; 3; 7.
|
|
|



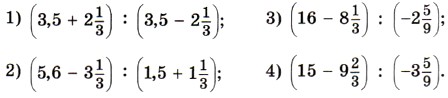
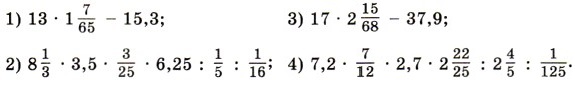
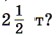
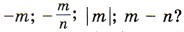
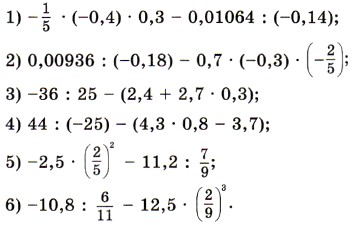
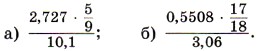
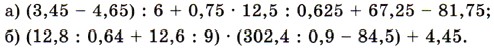
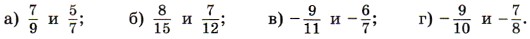
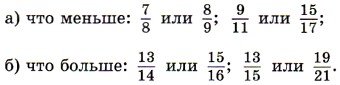
 раза.
раза.
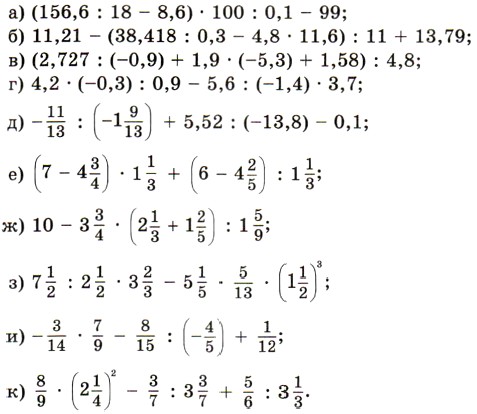
 до сотых?
до сотых?