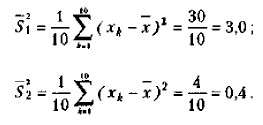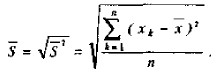|
|
|
|
|
Статистический анализ экспериментальных данных и способы наглядного представления результатов Методы первичной статистической обработки результатов экспериментаМетодами статистической обработки результатов эксперимента называются математические приемы, формулы, способы количественных расчетов, с помощью которых показатели, получаемые в ходе эксперимента, можно обобщать, приводить в систему, выявляя скрытые в них закономерности. Речь идет о таких закономерностях статистического характера, которые существуют между изучаемыми в эксперименте переменными величинами. Некоторые из методов математико-статистического анализа позволяют вычислять так называемые элементарные математические статистики, характеризующие выборочное распределение данных, например выборочное среднее, выборочная дисперсия, мода, медиана и ряд других. Иные методы математической статистики, например дисперсионный анализ, регрессионный анализ, позволяют судить о динамике изменения отдельных статистик выборки. С помощью третьей группы методов, скажем, корреляционного анализа, факторного анализа, методов сравнения выборочных данных, можно достоверно судить о статистических связях, существующих между переменными величинами, которые исследуют в данном эксперименте. Все методы математико-статистического анализа условно делятся на первичные и вторичные1. Первичными называют методы, с помощью которых можно получить показатели, непосредственно отражающие результаты производимых в эксперименте измерений. Соответственно под первичными статистическими показателями имеются в виду те, которые применяются в самих психодиагностических методиках и являются итогом начальной статистической обработки результатов психодиагностики. Вторичными называются методы статистической обработки, с помощью которых на базе первичных данных выявляют скрытые в них статистические закономерности. 1 Приводимые здесь определения и высказывания не всегда являются достаточно строгими с точки зрения теории вероятностей и математической статистики как сложившихся областей современной математики. Это сделано для лучшего понимания данного текста студентами, не подготовленными в области математики. К первичным методам статистической обработки относят, например, определение выборочной средней величины, выборочной дисперсии, выборочной моды и выборочной медианы. В число вторичных методов обычно включают корреляционный анализ, регрессионный анализ, методы сравнения первичных статистик у двух или нескольких выборок. Рассмотрим методы вычисления элементарных математических статистик, начав с выборочного среднего. Выборочное среднее значение как статистический показатель представляет собой среднюю оценку изучаемого в эксперименте психологического качества. Эта оценка характеризует степень его развития в целом у той группы испытуемых, которая была подвергнута психодиагностическому обследованию. Сравнивая непосредственно средние значения двух или нескольких выборок, мы можем судить об относительной степени развития у людей, составляющих эти выборки, оцениваемого качества. Выборочное среднее определяется при помощи следующей формулы:
где х — выборочная средняя величина или среднее арифметическое значение по выборке; n — количество испытуемых в выборке или частных психодиагностических показателей, на основе которых вычисляется средняя величина; хк — частные значения показателей у отдельных испытуемых. Всего таких показателей n, поэтому индекс k данной переменной принимает значения от 1 до n; Е — принятый в математике знак суммирования величин тех переменных, которые находятся справа от этого знака. Выражение Xх к соответственно означает сумму всех х с индексом k от 1 до n. П р и м е р. Допустим, что в результате применения психодиагностической методики для оценки некоторого психологического свойства у десяти испытуемых мы получили следующие частные показатели степени развитости данного свойства у отдельных испытуемых: x1 = 5, x2 = 4, х3 = 5, х4 = 6, x5 = 7, x6 = 3, Х7 = 6, х8 = 2, х9= 8, х10 = 4. Следовательно, n = 10, а индекс k меняет свои значения от 1 до 10 в приведенной выше формуле. Для данной выборки среднее значение2, вычисленное по этой формуле, будет равно:
2 В дальнейшем, как это и принято в математической статистике, с целью сокращения текста мы будем опускать слова «выборочное» и «арифметическое» и просто говорить о «среднем» или «среднем значении». В психодиагностике и в экспериментальных психолого-педагогических исследованиях среднее, как правило, не вычисляется с точностью, превышающей один знак после запятой, т.е. с большей, чем десятые доли единицы. В психодиагностических обследованиях большая точность расчетов не требуется и не имеет смысла, если принять во внимание приблизительность тех оценок, которые в них получаются, и достаточность таких оценок для производства сравнительно точных расчетов. Дисперсия как статистическая величина характеризует, насколько частные значения отклоняются от средней величины в данной выборке. Чем больше дисперсия, тем больше отклонения или разброс данных. Прежде чем представлять формулу для расчетов дисперсии, рассмотрим пример. Воспользуемся теми первичными данными, которые были приведены ранее и на основе которых вычислялась в предыдущем примере средняя величина. Мы видим, что все они разные и отличаются не только друг от друга, но и от средней величины. Меру их общего отличия от средней величины и характеризует дисперсия. Ее определяют для того, чтобы можно было отличать друг от друга величины, имеющие одинаковую среднюю, но разный разброс. Представим себе другую, отличную от предыдущей выборку первичных значений, например такую: 5, 4, 5, 6, 5, 6, 5, 4, 5, 5. Легко убедиться в том, что ее средняя величина также равна 5,0. Но в данной выборке ее отдельные частные значения отличаются от средней гораздо меньше, чем в первой выборке. Выразим степень этого отличия при помощи дисперсии, которая определяется по следующей формуле:
где S — выборочная дисперсия, или просто дисперсия;
n — количество испытуемых в выборке или первичных значений, по которым вычисляется дисперсия. Определим дисперсии для двух приведенных выше выборок частных значений, обозначив эти дисперсии соответственно индексами 1 и 2:
Мы видим, что дисперсия по второй выборке (0,4) значительно меньше дисперсии по первой выборке (3,0). Если бы не было дисперсии, то мы не в состоянии были бы различить данные выборки. Иногда вместо дисперсии для выявления разброса частных данных относительно средней используют производную от дисперсии величину, называемую выборочное отклонение. Оно равно квадратному корню, извлекаемому из дисперсии, и обозначается тем же самым знаком, что и дисперсия, только без квадрата— S:
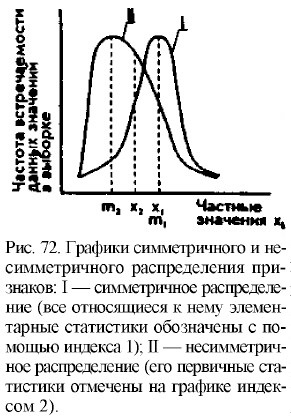
Медианой называется значение изучаемого признака, которое делит выборку, упорядоченную по величине данного признака, пополам. Справа и слева от медианы в упорядоченном ряду остается по одинаковому количеству признаков. Например, для выборки 2, 3, 4, 4, 5, 6, 8, 7, 9 медианой будет значение 5, так как слева и справа от него остается по четыре показателя. Если ряд включает в себя четное число признаков, то медианой будет среднее, взятое как полусумма величин двух центральных значений ряда. Для следующего ряда 0, 1,1, 2, 3, 4, 5, 5, 6, 7 медиана будет равна 3,5. Знание медианы полезно для того, чтобы установить, является ли распределение частных значений изученного признака симметричным и приближающимся к так называемому нормальному распределению. Средняя и медиана для нормального распределения обычно совпадают или очень мало отличаются друг от друга. Если выборочное распределение признаков нормально, то к нему можно применять методы вторичных статистических расчетов, основанные на нормальном распределении данных. В противном случае этого делать нельзя, так как в расчеты могут вкрасться серьезные ошибки. Если в книге по математической статистике, где Описывается тот или иной метод статистической обработки, имеются указания на то, что его можно применять только к нормальному или близкому к нему распределению признаков, то необходимо не укоснительно следовать этому правилу и полученное эмпирическое распределение признаков проверять на нормальность. Если такого указания нет, то статистика применима к любому распределению признаков. Приблизительно судить о том, является или не является полученное распределение близким к нормальному, можно, построив график распределения данных, похожий на те, которые представлены на рис. 72. Если график оказывается более или менее симметричным, значит, к анализу данных можно применять статистики, предназначенные для нормального распределения. Во всяком случае, допустимая ошибка в расчетах в данном случае будет относительно небольшой. Приблизительные картины симметричного и несимметричного распределений признаков показаны на рис. 72, где точками m1 и m2 на горизонтальной оси графика обозначены те величины признаков, которые соответствуют медианам, а х1 и x2 — те, которые соответствуют средним значениям.
Мода еще одна элементарная математическая статистика и характеристика распределения опытных данных. Модой называют количественное значение исследуемого признака, наиболее часто встречающееся в выборке. На графиках, представленных на рис. 72, моде соответствуют самые верхние точки кривых, вернее, те значения этих точек, которые располагаются на горизонтальной оси. Для симметричных распределений признаков, в том числе для нормального распределения, значение моды совпадает со значениями среднего и медианы. Для других типов распределений, несимметричных, это не характерно. К примеру, в последовательности значений признаков 1,2, 5,2,4, 2,6,7,2 модой является значение 2, так как оно встречается чаще других значений — четыре раза. Иногда исходных частных первичных данных, которые подлежат статистической обработке, бывает довольно много, и они требуют проведения огромного количества элементарных арифметических операций. Для того чтобы сократить их число и вместе с тем сохранить нужную точность расчетов, иногда прибегают к замене исходной выборки частных эмпирических данных на интервалы. Интервалом называется группа упорядоченных по величине значений признака, заменяемая в процессе расчетов средним значением. П р и м е р. Представим следующий ряд частных признаков: О, 1,1,2,2,3,3,3,4,4,5,5,5,5,6,6,6,7,7,8,8,8,9,9,9,10,10,11,11, 11. Этот ряд включает в себя 30 значений. Разобьем представленный ряд на шесть подгрупп по пять признаков в каждом. Первая подгруппа включит в себя первые пять цифр, вторая — следующие пять и т.д. Вычислим средние значения для каждой из пяти образованных подгрупп чисел. Они соответственно будут равны 1,2; 3,4; 5,2; 6,8; 8,6; 10,6. Таким образом, нам удалось свести исходный ряд, включающий тридцать значений, к ряду, содержащему всего шесть значений и представленному средними величинами. Это и будет интервальный ряд, а проведенная процедура — разделением исходного ряда на интервалы. Теперь все статистические расчеты мы можем производить не с исходным рядом признаков, а с полученным интервальным рядом, и результаты в равной степени будут относиться к исходному ряду. Однако число производимых в ходе расчетов элементарных арифметических операций будет гораздо меньше, чем количество тех операций, которые с этой же целью пришлось бы проделать в отношении исходного ряда признаков. На практике, составляя интервальный ряд, рекомендуется руководствоваться следующим правилом: если в исходном ряду признаков больше чем тридцать, то этот ряд целесообразно разделить на пять-шесть интервалов и в дальнейшем работать только с ними. Для проверки сказанного проведем пробное вычисление среднего значения по приведенному выше ряду, составляющему тридцать чисел, и по ряду, включающему только интервальные средние значения. Полученные цифры с точностью до двух знаков после запятой будут соответственно равны 5,97 и 5,97, т.е. являются одинаковыми.
|
|
|



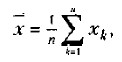
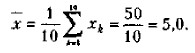
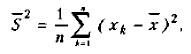
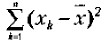 — выражение, означающее, что для всех хк от первого до последнего в данной выборке необходимо вычислить разности между частными и средними значениями, возвести эти разности в квадрат и просуммировать;
— выражение, означающее, что для всех хк от первого до последнего в данной выборке необходимо вычислить разности между частными и средними значениями, возвести эти разности в квадрат и просуммировать;