|
|
|
|
Главная >> Сборник задач по физике. 7—9 классы. Лукашик. ГДЗ |
|
|
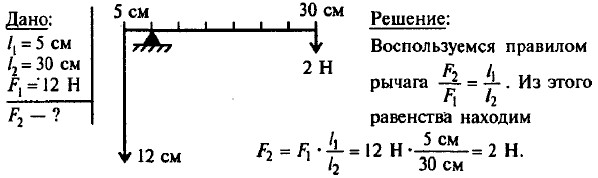
Рычаги Решения: Рычаги (продолжение)736. Мы знаем, что рычаг находится в равновесии, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки. Момент силы равен произведению величины силы на плечо. На рис. 206, а левое плечо рычага равно 1 делению, правое — 3 делениям. Поэтому мы можем записать равенство 1 • 3 Н = 3 • F. Отсюда сила F = 1 Н. На рис. 206, б левое плечо равно 2 делениям, правое — 1 делению. Слева подвешен груз массой 5 кг. Он действует на рычаг силой своего веса mg = 5 кг • 10 м/с2 = 50 Н. Таким образом, из условия равновесия получаем: 50 Н • 2 -F • 1. Отсюда F = 100 Н. 737. Судя по рисунку, грузы имеют одинаковый объем. Значит, при погружении в воду на них будут действовать одинаковые выталкивающие силы. В воздухе система грузов находится в равновесии. Левое плечо рычага l1 = 1 дел., правое плечо l2 = 3 дел. Условие равновесия: 3 Н • l1 = 1 Н • l2. В воде вес грузов уменьшится на величину выталкивающей силы Fв: P1 = 3 Н - Fв и Р2 = 1 Н - Fв. Момент силы, вращающей рычаг против часовой стрелки, станет равным M1 = P1 • l1 = (3H - Fв) • l1 = 3 H • l1 - Fв • l1. Момент силы, вращающей рычаг по часовой стрелке, будет М2 = P2 • l2 = (1 Н - Fв) • l2 = 1 H • l2 - Fв • l2. Напишем разность моментов: М1 • M2 = 3 Н • l1 - Fв • l1 - 1 Н • l2 + Fв • l2. Так как по условию 3 Н • l1 - 1 Н • l1, то М1 - М2 = Fв • l2 - Fв • l1 = Fв(l2 - l1). Поскольку l2 больше, чем l1, то разность моментов больше нуля. Таким образом, момент M1 больше момента М2. Равновесие нарушится и груз 3 Н опустится вниз. 738. На рис. 208 нанесены разные обозначения: 19,6 Н обозначает величину приложенной силы, а 1 кг обозначает массу подвешенного груза. Груз действует на правое плечо рычага силой своего веса P = mg= 1 кг • 9,8 м/с2 = 9,8 Н. Измерив плечи рычага, находим, что правое плечо рычага в два раза больше левого. Запишем это условие: lп = 2lл Момент силы, вращающей рычаг против часовой стрелки, равен Мп = 19,6 Н • lл. Момент силы, вращающей рычаг по часовой стрелке, будет Мп = 9,8 Н • lп = 9,8 Н • 2lл =19,6 Н • lл = Мл. Таким образом, мы получили равенство Мп = Мл, т. е. получили условие равновесия рычага. Значит, система находится в равновесии. 739. Если взяться за край ручки тисков, то увеличится момент силы затяжки, так как увеличится плечо силы. 740. В принципе, эта задача решается так же, как задача 736, б. Давайте для разнообразия решим ее, используя не правило моментов, а правило рычага. Оно гласит, что рычаг находится в равновесии, если приложенные к нему силы обратно пропорциональны их плечам: 741. Рычаг разбит на 6 делений. Значит, длина одного деления равна 60 см : 6 = 10 см. На рис. 210 изображен рычаг II-го рода. Условие его равновесия проще записывать через правило моментов. Сила 742. Пусть длина левого плеча l1 =20 см, а длина правого плеча равна l2. Нам нужно узнать величину l = l1 + l2. Воспользуемся правилом рычага 743. Динамометр растянут на 6 делений. Левое плечо рычага равно 6 делениям и к нему подвешен груз весом 2 Н. Правое плечо рычага равно 2 делениям. Пусть со стороны пружины динамометра на рычаг действует сила F. Тогда из условия равновесия по правилу моментов получаем равенство 6 дел. • 2 Н = 2 дел. • F Таким образом F = 6 Н и цена деления динамометра 6 Н : 6 = 1 Н. 744. Из рис. 213 видно, что отношение плеч рычага равно 745. Пусть со стороны динамометра на рычаг действует сила F На рис. 214, а показан рычаг первого рода. Видно, что отношение плеч рычага равно 746. Общий вес грузов составляет 3 Н. Плечо, на которое действует вес грузов, равно 4 делениям. Пусть со стороны динамометра на рычаг действует сила F. Найдем ее, используя правило моментов. Плечо силы нравно 6 делениям. Отсюда 6 дел. • F= 4 дел. • 3 Н. Получаем, что F = 2 Н. По третьему закону Ньютона сила, с которой динамометр действует на рычаг (приложена к рычагу), равна по величине силе, с которой рычаг действует на пружину (приложена к пружине). Таким образом, пружина натянута с силой 2 Н. Примечание. В этой задаче (и в других подобных с симметричным рычагом) весом рычага можно пренебрегать, а можно и не пренебрегать, так как симметричный рычаг и в отсутствие приложенных сил находится в равновесии. Следовательно, собственные моменты сил тяжести правой и левой его половин равны. При составлении уравнения моментов приложенных к рычагу сил эти собственные моменты сил тяжести войдут в правую и левую половины равенства в качестве дополнительных слагаемых и сократятся. 747.
<<< К началу Решения (окончание) >>>
|
|
|



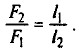 Пусть l1 = 1 дел., а l2 = 2 дел. Сила F1 равна весу груза массой m = 10 кг, т. е. F1 = mg = 10 кг • 10 м/с2 = 100 Н. Тогда
Пусть l1 = 1 дел., а l2 = 2 дел. Сила F1 равна весу груза массой m = 10 кг, т. е. F1 = mg = 10 кг • 10 м/с2 = 100 Н. Тогда 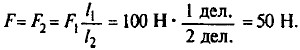
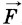 вращает рычаг против часовой стрелки. Ее момент равен М1 = F • l1 = F • 30 см. Груз своим весом Р врашает рычаг по часовой стрелке. Его момент равен М2 = P • l2 = 1 Н • 10 см. По условию равновесия М1 = М2 или F • 30 см = 2 Н • 10 см. Отсюда F = 2 Н : 3 ≈ 0,7 Н.
вращает рычаг против часовой стрелки. Ее момент равен М1 = F • l1 = F • 30 см. Груз своим весом Р врашает рычаг по часовой стрелке. Его момент равен М2 = P • l2 = 1 Н • 10 см. По условию равновесия М1 = М2 или F • 30 см = 2 Н • 10 см. Отсюда F = 2 Н : 3 ≈ 0,7 Н.
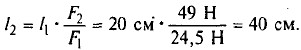 Окончательно, длина рычага равна
Окончательно, длина рычага равна 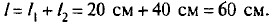
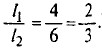 Если рычаг находится в равновесии, то по правилу рычага отношение сил
Если рычаг находится в равновесии, то по правилу рычага отношение сил 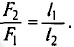 Пусть F1 = m1g и F2 = m2g. Тогда
Пусть F1 = m1g и F2 = m2g. Тогда 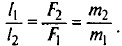 Отсюда находим массу противовеса
Отсюда находим массу противовеса 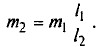 По условию m1 = 300 г и m2 • 300 г • 2/3 = 200 г.
По условию m1 = 300 г и m2 • 300 г • 2/3 = 200 г.
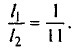 Из условия равновесия отношение приложенных сил будет
Из условия равновесия отношение приложенных сил будет 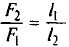 или
или 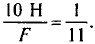 Получаем F = 100 Н. Динамометр растянут на 11 делений. Значит, цена деления 110 : 11 = 10 Н. На рис. 214,5 представлен рычаг второго рода. Сила в 10 Н вращает его против часовой стрелки. Плечо этой силы равно 12 делениям, а момент — 10 Н • 12 дел. Сила F со стороны динамометра вращает рычаг по часовой стрелке. Ее плечо равно 2-м делениям, а момент составляет F • 2 дел. По условию равновесия 10 Н • 12 дел. - F • 2 дел. Находим F = 60 Н. Динамометр растянут на 6 делений, следовательно, цена деления 60 Н : 6 — 10 Н.
Получаем F = 100 Н. Динамометр растянут на 11 делений. Значит, цена деления 110 : 11 = 10 Н. На рис. 214,5 представлен рычаг второго рода. Сила в 10 Н вращает его против часовой стрелки. Плечо этой силы равно 12 делениям, а момент — 10 Н • 12 дел. Сила F со стороны динамометра вращает рычаг по часовой стрелке. Ее плечо равно 2-м делениям, а момент составляет F • 2 дел. По условию равновесия 10 Н • 12 дел. - F • 2 дел. Находим F = 60 Н. Динамометр растянут на 6 делений, следовательно, цена деления 60 Н : 6 — 10 Н.