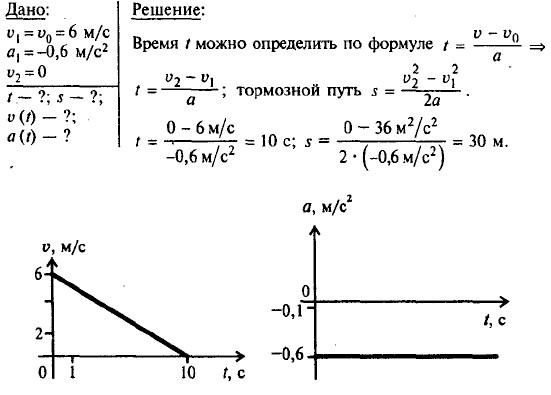
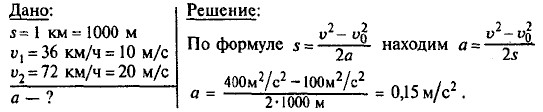|
|
|
|
Главная >> Сборник задач по физике. 7—9 классы. Лукашик. ГДЗ |
|
|
Глава II. Движение и взаимодействие тел Равномерное и неравномерное прямолинейное движение (решения окончание)151. I. x = x(t) - ? Уравнение зависимости координаты от времени имеет вид x = x0 + υxt (1), здесь х0 -гг начальная координата, т. е. положение тела в момент времени t = 0; На рисунке в учебнике графики движения трех тел. Для каждого из них надо определить x0 и υх и подставить их в формулу (1).
II. а) Для нахождения координат тел по графикам надо из точки t = 5 с восстановить перпендикуляр до пересечения с графиком и провести прямую перпендикулярную оси х. Итак, по графику через 5 секунд х1 =5 м; x2 = 0 (м); х3 = -7,5 (м). б) Чтобы найти координату тела через некоторое время по уравнению координаты надо в уравнение координаты поставить соответствующее время: x1 = 5 (м); x2 = 5 - 1 • 5 = 0 (м); х3 = -10 + 0,5 • 5 = -7,5 (м). III. Время и место встречи определяем по точке пересечения графиков. Перпендикуляры, опущенные из точки пересечения графиков на оси времени и координаты дают нам время и место встречи (tA; хА) : tA = 10 с; хА = -5 м. Второе и третье тела встретились через 10 с после начала движения в точке с координатой -5 м. 152. Нет. Ведь по определению при равномерном движении за равные промежутки времени тело должно проходить одинаковые отрезки пути. В условии задачи приведен пример равноускоренного движения. 153. График скорости равномерного прямолинейного движения — прямая, параллельная оси времени, так как скорость со временем не изменяется ни по величине ни по направлению (см. рис. в учебнике). Итак, графиком равномерного прямолинейного движения является график 4. Точка пересечения графиков 3 и 5 указывает, что примерно через 1,2 с после начала движения 3-го и 5-го тел скорости этих тел стали одинаковыми, но утверждать, что координаты тел стали одинаковыми, нельзя. 154. I. Начальные скорости движения — точки пересечения графиков функций с осью υ. Так υ01 = 0 (м/с); υ03 = 14 (м/с); υ04 = 8 (м/с). II. Приращение скорости за 1 с обозначим Δυ/Δt, здесь Δυ - изменение скорости за время Δt.
1) Первый график s = 1/2 • 6 • 12 = 36 (м), график функции 1 за 6 с дает нам треугольник υ1ср = 36 м : 6 с = 6 м/с. 2) третий график s = 1/2 • 6 • 17 = 51 м,
3) 4-й график s = 8 • 6 = 48 (м),
155.
156.
157. Зависимость скорости от времени имеет вид υ = υ0 + at, где υ0 — начальная скорость движения тела, а — ускорение движения. Рассмотрим каждый график в отдельности. 1) 2) 3) 4) 5) 158.
159.
160.
|
|
|



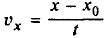 — скорость тела.
— скорость тела.

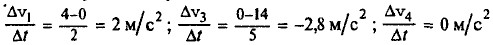 - скорость со временем не изменяется.
- скорость со временем не изменяется.

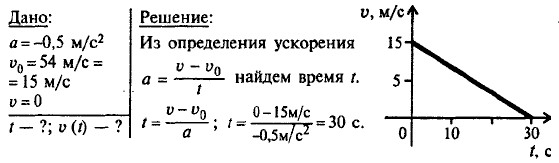
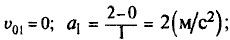 υ1 = 2t. Первое тело движется без начальной скорости равноускоренно с ускорением 2 м/с2.
υ1 = 2t. Первое тело движется без начальной скорости равноускоренно с ускорением 2 м/с2.
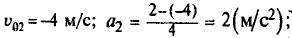 υ2 = -4 + 2 t. Второе тело движется с начальной скоростью — 4 м/с, с ускорением 2 м/с2.
υ2 = -4 + 2 t. Второе тело движется с начальной скоростью — 4 м/с, с ускорением 2 м/с2.
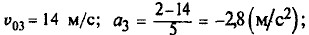 υ3 = 14 - 2,8 t. Третье тело движется с начальной скоростью 14 м/с равнозамедленно, с ускорением -2,8 м/с2.
υ3 = 14 - 2,8 t. Третье тело движется с начальной скоростью 14 м/с равнозамедленно, с ускорением -2,8 м/с2.
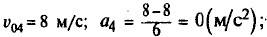 υ4 = 8. Четвертое тело движется равномерно со скоростью 8 м/с.
υ4 = 8. Четвертое тело движется равномерно со скоростью 8 м/с.
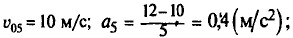 υ5 = 10 + 0,4 t. Пятое тело движется с начальной скоростью 10 м/с равноускоренно с ускорением 0,4 м/с2.
υ5 = 10 + 0,4 t. Пятое тело движется с начальной скоростью 10 м/с равноускоренно с ускорением 0,4 м/с2.