|
|
|
|
|
Глава 14. Электростатика § 99. Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»«Электроёмкость» — последняя тема раздела «Электростатика». При решении задач на эту тему могут потребоваться все сведения, полученные при изучении электростатики: закон сохранения электрического заряда, понятия напряжённости поля и потенциала, сведения о поведении проводников в электростатическом поле, о напряжённости поля в диэлектриках, о законе сохранения энергии применительно к электростатическим явлениям. Основной формулой при решении задач на электроёмкость является формула (14.22). Задача 1. Электроёмкость конденсатора, подключённого к источнику постоянного напряжения U = 1000 В, равна C1 = 5 пФ. Расстояние между его обкладками уменьшили в n = 3 раза. Определите изменение заряда на обкладках конденсатора и энергии электрического поля. Р е ш е н и е. Согласно формуле (14.22) заряд конденсатора q = CU. Отсюда изменение заряда Δq — (С2 - C)U = (nC1 - C1)U = (п — 1)С1U = 10-8 Кл. Изменение энергии электрического поля
Задача 2. Заряд конденсатора q = 3 • 10-8 Кл. Ёмкость конденсатора С = 10 пФ. Определите скорость, которую приобретает электрон, пролетая в конденсаторе путь от одной пластины к другой. Начальная скорость электрона равна нулю. Удельный заряд электрона Р е ш е н и е. Начальная кинетическая энергия электрона равна нулю, а конечная равна Следовательно, Окончательно
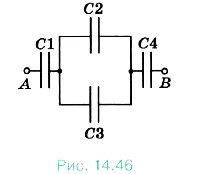
Задача 3. Четыре конденсатора ёмкостями С1 = С2 = = 1 мкФ, С3 = 3 мкФ, С4 = 2 мкФ соединены, как показано на рисунке 14.46. К точкам А и В подводится напряжение U = 140 В. Определите заряд q1 и напряжение U1, на каждом из конденсаторов. Р е ш е н и е. Для определения заряда и напряжения прежде всего найдём ёмкость батареи конденсаторов. Эквивалентная ёмкость второго и третьего конденсаторов С2,3 = С2 + С3, а эквивалентную ёмкость всей батареи конденсаторов, представляющей собой три последовательно соединённых конденсатора ёмкостями С1, С2,3, С4, найдём из соотношения 1/Cэкв = 1 /С1 + 1/С2,3 + 1 /С4, Сэкв = (4/7) • 10-6 Ф. Заряды на этих конденсаторах одинаковы: q1 = q2,3 = q4 = Сэкв = 8 • 10-5 Кл. Следовательно, заряд первого конденсатора q1 = 8 • 10-5 Кл, а разность потенциалов между его обкладками, или напряжение, U1 = q1/С1 = 80 В. Для четвёртого конденсатора аналогично имеем q4 = 8 • 10-5 Кл, U4 = q4/C4 = 40 В. Найдём напряжение на втором и третьем конденсаторах: U2 = U3 = q2,3/C2,3 = 20 В. Таким образом, на втором конденсаторе заряд q2 = C2U2 = 2 • 10-5 Кл, а на третьем конденсаторе q3 = C3U3 = 6 • 10-5 Кл. Отметим, что q2,3 = q2 + g3.
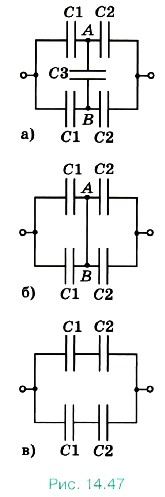
Задача 4. Определите эквивалентную электрическую ёмкость в цепи, изображённой на рисунке (14.47 а), если ёмкости конденсаторов известны. Р е ш е н и е. Часто при решении задач, в которых требуется определить эквивалентную электрическую ёмкость, соединение конденсаторов не очевидно. В этом случае если удаётся определить точки цепи, в которых потенциалы равны, то можно соединить эти точки или исключить конденсаторы, присоединённые к этим точкам, так как они не могут накапливать заряд (Δφ = 0) и, следовательно, не играют роли при распределении зарядов. В приведённой на рисунке (14.47, а) схеме нет очевидного параллельного или последовательного соединения конденсаторов, так как в общем случае φA ≠ φB в и к конденсаторам С1 и С2 приложены разные напряжения. Однако заметим, что в силу симметрии и равенства ёмкостей соответствующих конденсаторов потенциалы точек А и В равны. Следовательно, можно, например, соединить точки А и В. Схема преобразуется к виду, изображённому на рисунке (14.47, б). Тогда конденсаторы С1, так же как и конденсаторы С2, будут соединены параллельно и Сэкв определим по формуле 1/Сэкв = 1/2С1 + 1/2С2, откуда
Можно также просто не учитывать присутствие в схеме конденсатора СЗ, так как заряд на нём равен нулю. Тогда схема преобразуется к виду, изображённому на рисунке (14.47, в). Конденсаторы С1 и С2 соединены последовательно, следовательно,
Эквивалентные конденсаторы с С'экв соединены параллельно, так что окончательно получим такое же выражение для эквивалентной ёмкости:
Задача 5. Энергия плоского воздушного конденсатора W1 = 2 • 10-7 Дж. Определите энергию конденсатора после заполнения его диэлектриком с диэлектрической проницаемостью ε = 2, если: 1) конденсатор отключён от источника питания; 2) конденсатор подключён к источнику питания. Р е ш е н и е. 1) Так как конденсатор отключён от источника питания, то его заряд q0 остаётся постоянным. Энергия конденсатора до заполнения его диэлектриком Тогда Задачи для самостоятельного решения1. Разность потенциалов между обкладками конденсатора ёмкостью 0,1 мкФ изменилась на 175 В. Определите изменение заряда конденсатора. 2. В пространство между пластинами плоского конденсатора влетает электрон со скоростью 2-107 м/с, направленной параллельно пластинам конденсатора. На какое расстояние по направлению к положительно заряженной пластине сместится электрон за время движения внутри конденсатора, если длина конденсатора равна 0,05 м и разность потенциалов между пластинами 200 В? Расстояние между пластинами конденсатора равно 0,02 м. Отношение модуля заряда электрона к его массе равно 1,76 • 1011 Кл/кг. 3. Плоский конденсатор зарядили при помощи источника тока напряжением U = 200 В. Затем конденсатор был отключён от этого источника тока. Каким станет напряжение U1 между пластинами, если расстояние между ними увеличить от первоначального d = 0,2 мм до d1 = 0,7 мм? 4. Определите ёмкость воздушного сферического конденсатора. Радиусы сфер R1 и R2. 5. В плоский воздушный конденсатор вставляется металлическая пластина толщиной d0. Заряд на обкладках конденсатора q. Конденсатор отключён от источника. Расстояние между пластинами d, площадь пластин S. Определите изменение ёмкости конденсатора и энергии его электрического поля.
Повторите материал главы 14 по следующему плану1. Выпишите основные понятия и физические величины и дайте им определение. 2. Сформулируйте законы и запишите основные формулы. 3. Укажите единицы физических величин и их выражение через основные единицы СИ. 4. Опишите основные опыты, подтверждающие справедливость законов.
|
|
|



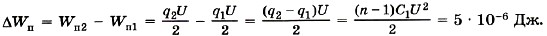
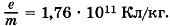
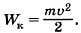 Применим закон сохранения энергии
Применим закон сохранения энергии 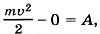 где А — работа электрического поля конденсатора:
где А — работа электрического поля конденсатора: 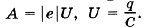
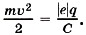
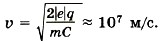
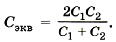
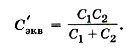
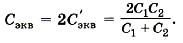
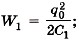 после заполнения
после заполнения 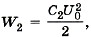 где С2 = εС1.
где С2 = εС1.
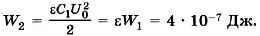
 Статическое электричество»
Статическое электричество»
 «Изготовление цилиндрического конденсатора. Исследование зависимости его электроёмкости от геометрических параметров и от наличия диэлектрика между пластинами. Определение электроёмкости конденсатора по зависимости q(U)»
«Изготовление цилиндрического конденсатора. Исследование зависимости его электроёмкости от геометрических параметров и от наличия диэлектрика между пластинами. Определение электроёмкости конденсатора по зависимости q(U)»