|
|
|
|
|
Глава 1. Электростатика § 1.11. Теорема Гаусса
Поток напряженности электрического поляПредварительно введем новую физическую величину — поток напряженности электрического поля. Напряженность поля характеризует электрическое поле в точке пространства. Поток напряженности зависит не от значения напряженности поля в данной точке, а от распределения поля по поверхности той или иной площади. Именно для этой величины формулируется теорема Гаусса. Выделим в поле элемент площадью ΔS. Он должен быть настолько малым, чтобы напряженность электрического поля во всех его точках можно было считать одинаковой. Проведем нормаль ΔN = EnΔS = Е • ΔS cos α. (1.11.1) Поток может быть положительным или отрицательным в зависимости от значения угла α.
Наглядно поток напряженности поля можно интерпретировать как величину, пропорциональную числу силовых линий, пронизывающих этот элемент. Линии, пронизывающие элемент ΔS, пронизывают также элемент ΔS0, представляющий собой проекцию ΔS на плоскость, перпендикулярную вектору
ΔN = Е cos α • ΔS = EΔS0, (1.11.2) так как ΔS0 = ΔS cos α. Если поле неоднородно и поверхность произвольна, то поток определяется так. Всю поверхность надо разбить на малые элементы площадью ΔSi, вычислить потоки напряженности через каждый из этих элементов, а потом просуммировать потоки через все элементы (рис. 1.38):
Так же определяется поток через замкнутую поверхность. За положительную нормаль к любому элементу замкнутой поверхности принимается внешняя нормаль, т. е. нормаль, направленная не внутрь поверхности, а наружу. Теорема Гаусса для точечного зарядаТеорема Гаусса устанавливает связь между потоком напряженности электрического поля через замкнутую поверхность и зарядом внутри этой поверхности. Вначале рассмотрим простой частный случай. Вычислим поток вектора Напряженность поля в каждой точке на поверхности сферы одна и та же по модулю, а проекция Еn равна:
Поток вектора
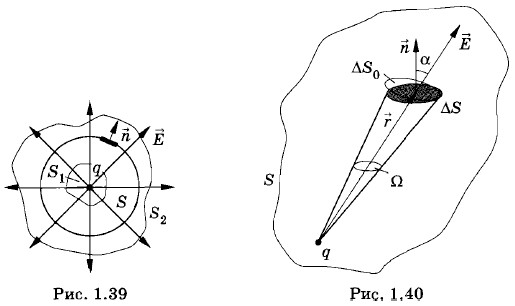
Этот результат, надо ожидать, справедлив и для любой замкнутой поверхности, содержащей заряд q. Ведь любую поверхность S1 или S2 (рис. 1.39) пронизывает то же число силовых линий, что и поверхность S. Таким образом, согласно теореме Гаусса, поток напряженности через замкнутую поверхность пропорционален электрическому заряду внутри этой поверхности. Теперь дадим более строгое доказательство теоремы для одного точечного заряда, охватываемого произвольной замкнутой поверхностью площадью S (рис. 1.40). Выделим на этой поверхности малый элемент ее ΔS. Поток напряженности через этот элемент равен:
где r — расстояние от элемента ΔS до заряда q, т. е. модуль радиуса-вектора, указывающего положение элемента ΔS относительно заряда q. Согласно (1.11.2), ΔS cos α = ΔS0, где ΔS0 — проекция площадки ΔS на плоскость, перпендикулярную радиусу-вектору
|
|
|



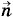 к элементу. Направление этой нормали выбирается произвольно (рис. 1.36). Угол между векторами
к элементу. Направление этой нормали выбирается произвольно (рис. 1.36). Угол между векторами 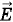 и
и 
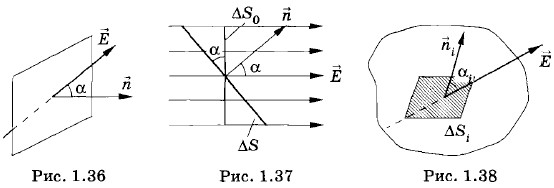


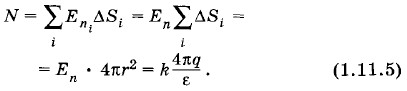
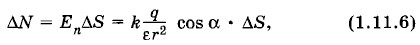
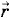 . Так как ΔS очень мала, то ΔS0 фактически есть проекция AS на поверхность сферы. Следовательно, уравнение (1.11.6) можно переписать так:
. Так как ΔS очень мала, то ΔS0 фактически есть проекция AS на поверхность сферы. Следовательно, уравнение (1.11.6) можно переписать так:
