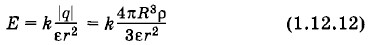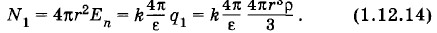|
|
|
|
|
Глава 1. Электростатика Поле заряженной плоскости, сферы и шараПоле равномерно заряженного шараДля характеристики распределения заряда по объему используется понятие объемной плотности заряда. Объемной плотностью заряда называется отношение заряда Δq к объему ΔV, в котором он распределен:
Эта плотность может непрерывно изменяться внутри заряженного тела. Если заряд q равномерно распределен по объему V, то объемная плотность заряда постоянна и равна:
Будем считать, что шар радиусом R равномерно заряжен; плотность заряда ρ известна. Полный заряд шара
(при условии, что r ≥ R). Поле аналогично полю точечного заряда q, расположенного в центре шара.
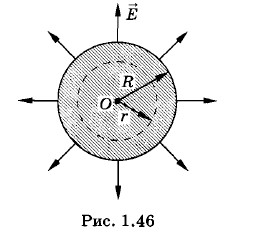
Для нахождения поля внутри шара нужно применить теорему Гаусса к потоку напряженности через сферическую поверхность радиусом r < R (рис. 1.46). Заряд q1 внутри этой поверхности равен:
Поток напряженности через эту поверхность, согласно теореме Гаусса*, равен:
* Мы предполагаем, что диэлектрическая проницаемость среды одинакова внутри и вне шара. Отсюда для напряженности поля внутри шара получим выражение:
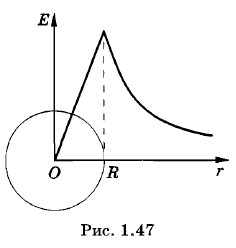
Напряженность электрического поля линейно растет с увеличением расстояния вплоть до r = R. При r > R она определяется формулой (1.12.12). График модуля напряженности поля в зависимости от расстояния до центра представлен на рисунке 1.47.
Заряженный лист фольги имеет такие же размеры, как страница из тетради. Можно ли определить напряженность электрического поля, созданного листом, на расстоянии 0,5 см от него, используя формулу (1.12.4)?
|
|
|





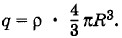 Напряженность электрического поля вне шара можно найти с помощью теоремы Гаусса точно так же, как и напряженность равномерно заряженной сферы [см. формулу (1.12.9)]:
Напряженность электрического поля вне шара можно найти с помощью теоремы Гаусса точно так же, как и напряженность равномерно заряженной сферы [см. формулу (1.12.9)]: