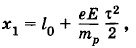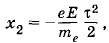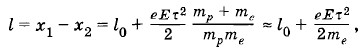|
|
|
|
|
Глава 1. Электростатика § 1.16. Примеры решения задачПри решении задач с использованием понятия напряженности электрического поля необходимо знать формулы (1.9.3) и (1.9.5), определяющие силу, действующую на заряд со стороны электрического поля, и напряженность поля точечного заряда. Пользуясь принципом суперпозиции полей, можно вычислить напряженность поля заряженного тела с произвольно распределенным в пространстве зарядом. Этот заряд следует рассматривать как совокупность точечных зарядов. Полезно помнить формулы напряженности поля равномерно заряженной сферы (1.12.9) и равномерно (по объему) заряженного шара (1.12.15), а также поля равномерно заряженной плоскости (1.12.4). Очень важно уметь свободно пользоваться понятием линий напряженности, дающих качественную картину распределения поля в пространстве. Также необходимо хорошо знать поведение проводников и диэлектриков в электростатическом поле. Задача 1Положительный заряд q равномерно распределен по тонкому проволочному кольцу радиусом R. Найдите напряженность электрического поля на оси кольца в зависимости от расстояния h от центра кольца.
Решение. Напряженность Заряд малого элемента кольца
Следовательно, модуль напряженности поля, создаваемого элементом кольца в точке А, равен:
Вследствие симметрии суммарный вектор
Из рисунка видно, что
Сумма
Из этого выражения вытекает, что в центре кольца (h = 0) Е = 0. Задача 2Свойства электрического диполя (системы из двух точечных зарядов +|q| и -|q|, находящихся на расстоянии l друг от друга) характеризуются его электрическим моментом а) точка лежит на прямой, проходящей через ось диполя;
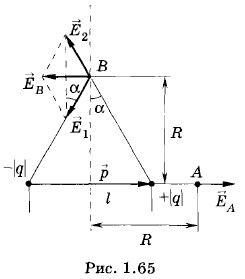
Решение. а) В первом случае, как это видно из рисунка 1.65, напряженность поля в точке А равна:
Следовательно, модуль вектора напряженности в точке А
Направлен вектор
б) Во втором случае (см. рис. 1.65) напряженность поля, со зданного каждым из зарядов в точке В, равна:
Суммарный вектор напряженности
Заметим, что в обоих случаях напряженность убывает как Задача 3
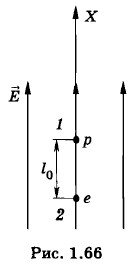
В сильном однородном электрическом поле напряженностью Решение. Направим ось X по направлению силовой линии
где е — заряд, а mр — масса протона. Координата электрона
где me — масса электрона. Искомое расстояние
так как mp » me.
|
|
|



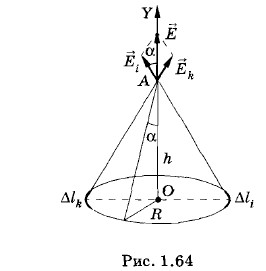
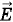 поля в произвольной точке А на оси кольца равна геометрической сумме напряженностей (принцип суперпозиции), создаваемых отдельными малыми элементами длиной Δli заряженного кольца (рис. 1.64).
поля в произвольной точке А на оси кольца равна геометрической сумме напряженностей (принцип суперпозиции), создаваемых отдельными малыми элементами длиной Δli заряженного кольца (рис. 1.64).
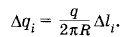
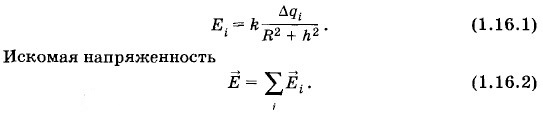
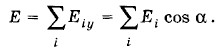
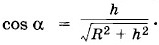 Следовательно, с учетом
Следовательно, с учетом
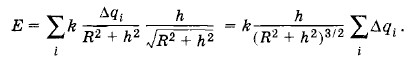
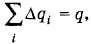 поэтому окончательно имеем:
поэтому окончательно имеем:
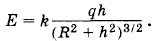
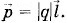 Найдите напряженность поля электрического диполя с моментом
Найдите напряженность поля электрического диполя с моментом 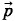 в точке, отстоящей от центра оси диполя на расстоянии R » l в двух случаях:
в точке, отстоящей от центра оси диполя на расстоянии R » l в двух случаях:
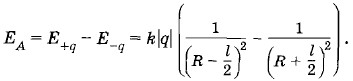
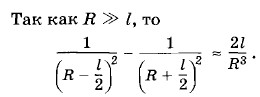
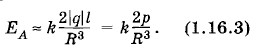
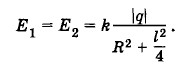
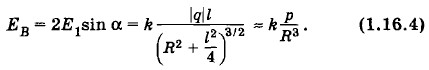
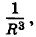 т. е. быстрее, чем напряженность поля точечного заряда (пропорциональная
т. е. быстрее, чем напряженность поля точечного заряда (пропорциональная 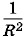 ).
).