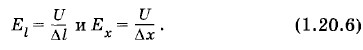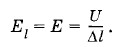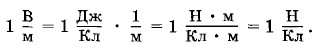|
|
|
|
|
Глава 1. Электростатика 1.20. Связь между напряженностью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности
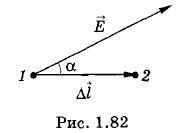
Напряженность и разность потенциаловРабота поля при малом перемещении А = qEΔlcos α = qElΔl, (1.20.1)
где α — угол между векторами С другой стороны, согласно уравнению (1.19.6), A = -qΔφ, (1.20.2) где Δφ = φ2 - φ1 — изменение потенциала при перемещении заряда из точки 1 в точку 2 (см. рис. 1.82). Приравнивая выражения для работы (1.20.1) и (1.20.2), найдем: ElΔl = -Δφ. (1.20.3) Следовательно, зная напряженность поля в каждой точке, можно вычислить изменение потенциала между любыми точками. А зная изменение потенциала между любыми сколь угодно близкими точками в поле, связанными вектором перемещения
Используя выражение для работы (1.18.1) в форме скалярного произведения, можно получить выражение для проекции напряженности электрического поля на ось X:
Здесь Δφ — изменение потенциала между точками с координатами x1 и х2 (Δx = х2 - x1). Аналогичные выражения можно написать для проекций напряженности поля на другие оси координат. В случае однородного поля перемещение Δl или изменение координаты Δx в формулах (1.20.4) и (1.20.5) могут быть любыми. Если вместо изменения потенциала использовать разность потенциалов U = -Δφ, то эти формулы можно записать так:
Формулы (1.20.4), (1.20.5) или (1.20.6) показывают, что чем меньше меняется потенциал на расстоянии Δl или Δx, тем меньше напряженность электрического поля. Если потенциал не меняется совсем, то напряженность поля равна нулю. Напряженность электростатического поля направлена в сторону убывания потенциала. Действительно, если φ(x2) < φ(x1), то, согласно формуле (1.20.5), Ех > 0. Это и означает, что напряженность поля направлена от точки с координатой х1 к точке с координатой x2. Единица напряженности электрического поляЕдиницу напряженности электрического поля в СИ устанавливают на основе единицы разности потенциалов. Для этого можно использовать формулу (1.20.6) для случая, когда вектор
Напряженность электрического поля равна единице, если разность потенциалов между двумя точками на расстоянии 1 м в однородном поле равна 1 В. Наименование этой единицы — вольт на метр (В/м). Как уже говорилось, напряженность можно также выражать в ньютонах на кулон. Действительно,
|
|
|



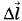 заряда q равна:
заряда q равна:
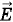 и
и