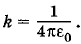|
|
|
|
|
Глава 1. Электростатика § 1.24. Электрическая емкость
Такого рода задачи встречаются очень часто не только в электростатике, но и при изучении электрического тока. Для их решения вводят особую физическую величину — электрическую емкость, или просто емкость. Электрическая емкость уединенного проводникаРассмотрим сферический проводник радиусом r. Пусть он находится очень далеко от других тел, так что его размеры во много раз меньше расстояний до этих тел. Такой проводник называют уединенным. При сообщении шару заряда q в окружающем пространстве возникнет электростатическое поле. Потенциал шара изменится и станет равным ф. Если потенциал бесконечно удаленных точек поля принять равным нулю, то потенциал шара можно вычислить по формуле (1.19.4). Поэтому отношение заряда шара к его потенциалу
не зависит от заряда и определяется лишь радиусом шара и диэлектрической проницаемостью ε окружающей среды. Замечательным является то, что не только для шара, но и для уединенного проводника произвольной формы потенциал прямо пропорционален заряду. Поэтому отношение заряда проводника к его потенциалу не зависит от значения заряда и определяется лишь геометрическими размерами проводника, его формой и электрическими свойствами окружающей среды (диэлектрической проницаемостью ε). Это позволяет ввести понятие электрической емкости уединенного проводника. Электрической емкостью С проводника называется отношение заряда q проводника к его потенциалу φ:
Емкость выражается через отношение заряда к потенциалу, но не зависит ни от того, ни от другого. Точно так же, например, скорость при равномерном прямолинейном движении выражается через отношение пути ко времени: Емкость не зависит от материала проводника: железные, медные тела и тела из других материалов одинаковых размеров и формы имеют одинаковую емкость. Термин «электрическая емкость» возник по аналогии с емкостью сосуда. Чем больше емкость проводника, тем меньше меняется его потенциал при сообщении заряда. Точно так же, чем больше площадь основания цилиндрического сосуда, тем меньше меняется уровень жидкости в нем при добавлении определенного количества жидкости. Практическая польза понятия емкости состоит в том, что, определив емкость проводника экспериментально или вычислив ее теоретически, можно с помощью формулы (1.24.2) найти потенциал проводника по известному заряду или, наоборот, заряд по известному потенциалу. Емкость шараСогласно определению емкости (1.24.2) и формуле (1.24.1) электрическая емкость шара в СИ равна:
так как в этой системе В системе СГСЭ потенциал шара вычисляется по формуле (1.19.4), тогда при k = 1 и в соответствии с определением (1.24.2) С = εr. (1.24.4) В вакууме емкость проводящего шара в системе СГСЭ равна его радиусу.
|
|
|





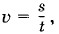 но не зависит ни от пути s, ни от времени t, так как является постоянной величиной.
но не зависит ни от пути s, ни от времени t, так как является постоянной величиной.