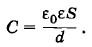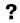|
|
|
|
|
Глава 1. Электростатика КонденсаторыИзмерение диэлектрической проницаемостиЗависимость емкости конденсатора от электрических свойств вещества между его обкладками используется для измерения диэлектрической проницаемости вещества. Для этого нужно экспериментально определить отношение емкостей конденсатора с диэлектрической пластиной между обкладками (С) и без нее (С0). Как следует из выражения (1.25.3), диэлектрическая проницаемость
Емкость сферического конденсатораВ заключение вычислим емкость еще одного типа конденсаторов — сферического конденсатора. Обкладками конденсатора являются две сферы: внутренняя радиусом R1 и внешняя радиусом R2 (см. рис. 1.98). Потенциал внешней обкладки равен сумме потенциалов, создаваемых зарядом +q на внешней обкладке и -q на внутренней (принцип суперпозиции). Потенциал заряженной сферы равен потенциалу точечного заряда, помещенного в центре сферы. Поэтому
при условии, что потенциал на бесконечности принят равным нулю. Наглядно это объясняется так. Конденсатор не создает поля во внешнем пространстве, Поэтому потенциал во всех точках вне наружной сферы один и тот же. На бесконечности он равен нулю. Значит, он равен нулю и во всех точках, включая поверхность внешней сферы. Потенциал внутренней сферы
Здесь учтено, что заряд на внешней сфере создает внутри нее (1.25.5) постоянный потенциал Разность потенциалов
Если зазор между обкладками d = R2 - R1 мал по сравнению R1 и R2, то
А это есть формула для емкости плоского конденсатора. Такой результат и следовало ожидать. Если же R2 → ∞, то в СИ С = 4πε0εR1. Это емкость уединенного шара.
1. Чему равна емкость стеклянного шарика радиусом 1 см? 2. Какую форму должен иметь сосуд, чтобы между его емкостью и электрической емкостью существовала бы количественная аналогия?
|
|
|




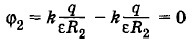
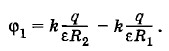
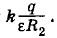
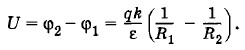

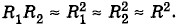 Учитывая, что площадь поверхности сферы S = 4πR2, вместо формулы (1.25.7) приближенно будем иметь:
Учитывая, что площадь поверхности сферы S = 4πR2, вместо формулы (1.25.7) приближенно будем иметь: