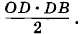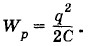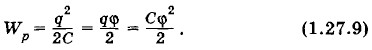|
|
|
|
|
Глава 1. Электростатика § 1.27. Энергия заряженных конденсаторов и проводников. Применения конденсаторов
Энергия плоского конденсатора
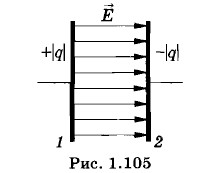
Выведем формулу для энергии плоского конденсатора. Напряженность поля, созданного зарядом одной из пластин, равна В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины (рис. 1.105). Согласно формуле (1.18.4) для потенциальной энергии заряда в однородном поле энергия конденсатора равна:
где q — заряд конденсатора, a d — расстояние между пластинами*. Формула (1.18.4) справедлива для энергии точечного заряда в однородном поле. Но заряд на пластине можно мысленно разделить на малые элементы Δq. Энергия каждого элемента равна: Так как Ed = U, где U разность потенциалов между обкладками конденсатора, то его энергия равна:
Эта энергия равна работе, которую совершит электрическое поле при сближении пластин вплотную. Заменив в формуле (1.27.2) либо разность потенциалов, либо заряд с помощью выражения (1.25.1) для емкости конденсатора, получим:
Энергия произвольного конденсатораФормулы (1.27.3) справедливы для энергии любого конденсатора, а не только плоского. Докажем это, используя более общий метод вычисления энергии. Зарядку конденсатора в принципе можно осуществить так. Будем постепенно малыми порциями -Δq переносить отрицательный заряд с одной пластины на другую. При этом конденсатор будет заряжаться, а электрическое поле внутри него совершать работу. Если порция заряда -Δq мала, то можно считать, что напряжение U = φ1 - φ2 между его пластинами во время переноса заряда не меняется. Тогда работа ΔА, согласно формуле (1.19.8), равна: ΔA = -ΔqU. (1.27.4)
Изменение энергии конденсатора в соответствии с формулой (1.17.1) равно:
Поле совершает отрицательную работу (ΔА < 0), а потенциальная энергия растет (ΔWр > 0). На графике зависимости Следовательно,
Это выражение совпадает с формулой (1.27.3) для энергии плоского конденсатора, выраженной через заряд и емкость. При данном выводе было совершенно несущественно, что конденсатор — плоский. Энергия заряженного проводникаЛюбой заряженный проводник, подобно заряженному конденсатору, обладает энергией*. * Конечно, энергией обладает и заряженный диэлектрик, но вычислить его энергию сложно. Для проводника это сделать нетрудно, так как все его точки имеют одинаковый потенциал. Будем заряжать проводник, перемещая к нему из бесконечности электрический заряд малыми порциями Δq. Все дальнейшие рассуждения подобны использованным выше для вычисления энергии конденсатора. При перемещении заряда Δq электрическое поле проводника совершает работу ΔА = Δq(φ∞ - φ), (1.27.7) где φ — потенциал проводника, имеющего заряд q. Потенциал на бесконечности считаем равным нулю (φ∞ = 0). Тогда
где С — емкость проводника. В результате энергия заряженного проводника
В отличие от формул (1.27.3) здесь φ — потенциал проводника (вместо напряжения U), а С — емкость уединенного тела, а не конденсатора.
|
|
|



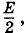 , где Е — напряженность поля в конденсаторе (см. § 1.25).
, где Е — напряженность поля в конденсаторе (см. § 1.25).

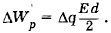

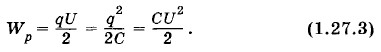
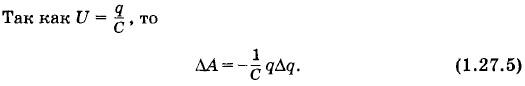
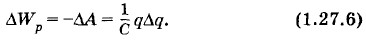
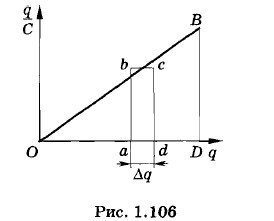
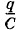 от q (рис. 1.106) приращение энергии ΔWp численно равно площади прямоугольника abcd со сторонами
от q (рис. 1.106) приращение энергии ΔWp численно равно площади прямоугольника abcd со сторонами