|
|
|
|
|
Глава 2. Постоянный электрический ток § 2.2. Плотность тока. Сила тока
Плотность тока
Введем понятие плотности электрического тока для наиболее простого случая упорядоченного движения одинаковых заряженных частиц. Выделим в среде, в которой существует ток, очень малый объем в форме прямого цилиндра с площадью основания ΔS (рис. 2.5). Цилиндр ориентирован так, что его основания перпендикулярны скорости упорядоченного движения частиц
Средняя скорость хаотически движущихся частиц равна нулю. Высота цилиндра пусть равна пути υΔt, проходимому частицами за время Δt. Здесь υ — модуль скорости упорядоченного движения частиц. Тогда все заряженные частицы, находящиеся внутри цилиндра, за время Δt пересекут правое основание цилиндра с площадью ΔS. Если концентрация заряженных частиц в среде n, то за время Δt через сечение с площадью ΔS будет перенесен заряд Δq = q0nυΔtΔS, где q0 — заряд отдельной частицы. Вектором плотности тока
где р = q0n — пространственная плотность электрического заряда. В случае движения отрицательно заряженных частиц (q0 < 0) векторы Сила токаВектор плотности тока представляет собой локальную (или дифференциальную) характеристику тока: он определяет переносимый заряд через малую площадку в проводящей среде и направление движения заряженных частиц. Введем теперь полную для всего сечения характеристику тока — силу тока*. * Термин сила тока нельзя считать удачным, так как слово «сила», применяемое к току, не имеет никакого отношения к понятию «сила» в механике. Но термин «сила тока» был введен давно и утвердился в науке. Силой тока называют отношение заряда Δq, переносимого через поперечное сечение проводника площадью S за промежуток времени Δt, к этому промежутку:
Формула (2.2.3) выражает среднее за время Δt значение силы тока. Сила тока в данный момент — мгновенная сила тока — представляет собой предел отношения электрического заряда Δq, прошедшего через поперечное сечение проводника за малый промежуток времени Δt, к этому промежутку при Δt, стремящемуся к нулю:
Если за любые равные между собой промежутки времени через поперечное сечение проводника проходят одинаковые заряды, т. е. если сила тока не изменяется с течением времени, то электрический ток называют постоянным. Сила постоянного тока численно равна заряду, проходящему через поперечное сечение проводника за 1 с:
Сила тока, подобно заряду, может быть как положительной, так и отрицательной. Знак силы тока зависит от того, какое из направлений вдоль проводника принято за положительное. Сила тока I > 0, если направление тока совпадает с условно выбранным положительным направлением вдоль проводника. В противном случае I < 0. Сила тока однозначно выражается через плотность тока. В частном случае при равномерном распределении плотности тока по сечению проводника сила тока I = jnS, (2.2.6)
где jn = jcos α — проекция вектора плотности тока на нормаль I = jS = |q0|nυS (2.2.7) выражается положительным числом. Таким образом, сила тока в проводнике прямо пропорциональна заряду, переносимому каждой частицей, концентрации частиц, скорости их направленного движения и площади поперечного сечения проводника.
|
|
|



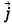 и скалярной величиной — силой тока I.
и скалярной величиной — силой тока I.
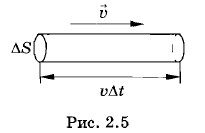
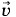 Под скоростью упорядоченного движения частиц в малом объеме ΔV (но содержащем много частиц) мы понимаем отношение геометрической суммы скоростей частиц к числу их в этом объеме:
Под скоростью упорядоченного движения частиц в малом объеме ΔV (но содержащем много частиц) мы понимаем отношение геометрической суммы скоростей частиц к числу их в этом объеме:
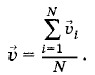
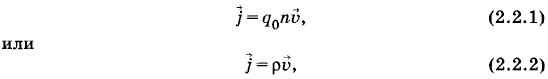
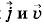 направлены противоположно друг другу. Если среда однородна, то модуль плотности тока численно равен электрическому заряду, переносимому в единицу времени через единичную площадку, перпендикулярную скорости
направлены противоположно друг другу. Если среда однородна, то модуль плотности тока численно равен электрическому заряду, переносимому в единицу времени через единичную площадку, перпендикулярную скорости 


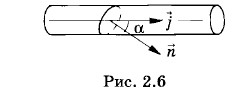
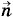 к плоскости сечения проводника, а S — площадь этого сечения (рис. 2.6). Направление нормали
к плоскости сечения проводника, а S — площадь этого сечения (рис. 2.6). Направление нормали