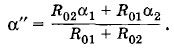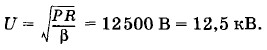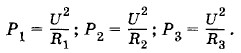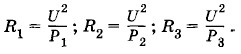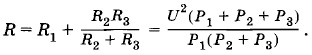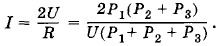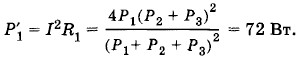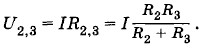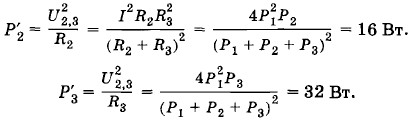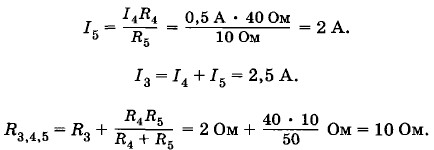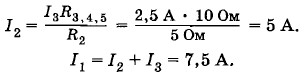|
|
|
|
|
Глава 2. Постоянный электрический ток
§ 2.10. Примеры решения задачВ задачах на материал предыдущих параграфов главы используется закон Ома (2.4.3), а также формулы (2.4.6), (2.5.1) и (2.5.2) для зависимости сопротивления от свойств проводника и температуры. При решении задач на работу и мощность тока надо применять формулы (2.7.1)—(2.7.7). В задачах на тепловое действие тока используется закон Джоуля—Ленца. Причем формулой Q = I2RΔt удобно пользоваться для последовательного соединения проводников, так как сила тока в этом случде одинакова во всех проводниках. При параллельном соединении проводников удобна формула При решении задач на электрические цепи постоянного тока надо, как правило, нарисовать схему цепи и выяснить, какие проводники соединены между собой последовательно, какие — параллельно, и воспользоваться необходимыми формулами для последовательного и параллельного соединения проводников (2.8.3)—(2.8.15). В более сложных случаях, когда в схеме невозможно выделить последовательно и параллельно соединенные проводники, следует попытаться найти точки с одинаковыми потенциалами. Эти точки можно или разъединить, исключив соединяющие их проводники, или соединить в общий узел. Токи в электрической цепи от этого не изменятся, так как между такими точками ток не идет. Точки с равными потенциалами легко найти в схемах, обладающих симметричными контурами. После соединения или разъединения точек с равными потенциалами обычно получается эквивалентная схема, состоящая из последовательно и параллельно соединенных проводников. Однако встречаются сложные схемы, в которых не существует точек с одинаковыми потенциалами. Решение таких задач требует некоторой изобретательности (см. решение задачи 9). Задача 1Плоский воздушный конденсатор с квадратными пластинами (сторона пластины а = 20 см) равномерно погружается в жидкий диэлектрик (ε = 3,3) так, что пластины оказываются перпендикулярными уровню жидкости. Расстояние между пластинами d = 2,5 мм. К конденсатору подключен источник постоянного напряжения U = 100 В. Какова сила тока в проводах, соединяющих пластины с полюсами источника, в процессе погружения конденсатора в диэлектрик со скоростью υ = 0,5 м/с? Решение. Сила тока, согласно формуле (2.2.3), равна:
Найдем изменение заряда Δq на одной из пластин конденсатора за время Δt полного его погружения в диэлектрик. В момент начала погружения заряд на пластине конденсатора
где ε0 = 8,85 • 10-12 Ф/м — электрическая постоянная. В конце погружения заряд на пластине конденсатора
Следовательно,
Задача 2Удельное сопротивление графитового стержня от карандаша ρ = 4 • 10-4 Ом • м. Чему равна сила тока I в стержне, если к его концам приложено напряжение U = 6 В? Длина стержня l = 20 см, его диаметр d = 2 мм. Решение. По закону Ома
Задача 3Два проводника с температурными коэффициентами сопротивления α1 и α2 имеют при 0 °С сопротивления R01 и R02. Чему равен температурный коэффициент сопротивления проводника, составленного из двух данных проводников, соединенных: а) последовательно; б) параллельно? Решение. Согласно соотношению (2.5.1) сопротивления проводников при температуре t соответственно равны: R1 = R01(1 + α1t), R2 = R02(1 + α2t) а) При последовательном соединении, согласно формуле (2.8.6), общее сопротивление R = R1 + R2 = R01 + R02 + (α1R01 + α2R02)t С другой стороны, можно написать: R = R0(1 + α't), где R0 = R01 + R02, а α' — искомый температурный коэффициент. Отсюда
б) При параллельном соединении, согласно формуле (2.8.13), общее сопротивление
где
Задача 4Линия электропередачи имеет сопротивление R = 250 Ом. Какое напряжение должно быть на зажимах генератора для того, чтобы при передаче по этой линии к потребителю мощности Р = 25 кВт потери в линии не превышали β = 4% передаваемой потребителю мощности? Решение. Передаваемая мощность P = IU, (2.10.1) где I — сила тока в линии, a U — искомое напряжение. Потери мощности в линии электропередачи Pпотерь = βP = βIU. (2.10.2) С другой стороны, Pпотерь = I2R. (2.10.3) Из равенств (2.10.2) и (2.10.3) находим:
Подставляя найденное значение силы тока в выражение для передаваемой мощности (2.10.1), получим:
Задача 5
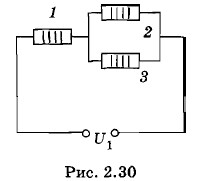
Три нагревательных прибора мощностью Р1 = 50 Вт, Р2 = 25 Вт и Р3 = 50 Вт, рассчитанные на напряжение U = 110 В каждый, соединены, как показано на рисунке 2.30, и включены в сеть с напряжением U1 = 2U = 220 В. Определите мощность, выделяемую каждым нагревательным прибором. Решение. Номинальные мощности приборов, согласно формуле (2.7.7), равны соответственно:
Отсюда находим сопротивления приборов (в рабочем состоянии):
Если не учитывать изменение сопротивления приборов при их работе, то общее сопротивление всех нагревательных приборов
Сила тока в цепи (и в нагревательном элементе)
Мощность P'1 выделяемую прибором 1, удобно найти по формуле (2.7.6):
Напряжение на нагревательных элементах 2 и 3 по закону Ома равно:
Теперь найдем мощность, выделяемую приборами 2 и 3:
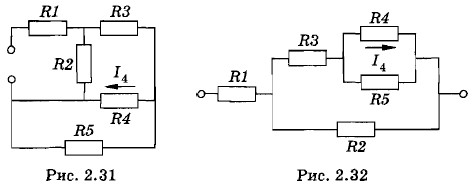
Задача 6В цепи, схема которой изображена на рисунке 2.31, сопротивления всех резисторов известны и равны соответственно R1 = 2 Ом, R2 = 5 Ом, R3 = 2 Ом, R4 = 40 Ом, R5 = 10 Ом. Сила тока в резисторе R4 I4 = 0,5 А. Определите силу тока во всех остальных резисторах и напряжение на зажимах цепи. Решение. Решение задачи значительно облегчается, если приведенную на рисунке 2.31 схему заменить эквивалентной (рис. 2.32).
В задачах на сложное соединение большого количества резисторов расчеты в общем виде можно не производить. Проще для каждой величины сразу получать числовой ответ. Найдем силу тока в резисторе R5. Она равна напряжению на разветвлении 4—5, деленному на R5:
Отсюда
Напряжение на зажимах цепи U = I1R1 + I2R2 = 7,5 А • 2 Ом + 5 А • 5 Ом = 40 В. Итак, I1 = 7, 5 А; I2 = 5 А; I3 = 2,5 А; I5 = 2 A; U = 40 В.
|
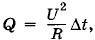так как в этом случае одинаково напряжение на всех проводниках.
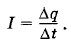
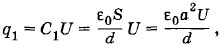
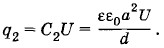
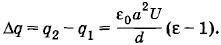Время погружения
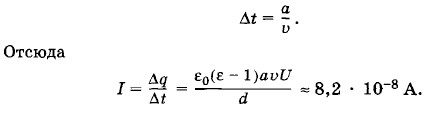
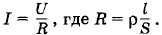(2.4.3) Площадь поперечного сечения стержня 
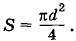Следовательно,
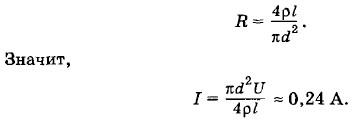
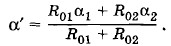
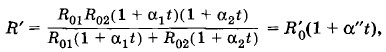
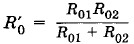— сопротивление параллельно соединенных проводников при 0 °С. Пренебрегая членами, пропорциональными произведениям температурных коэффициентов, как малыми, получим:
|
|