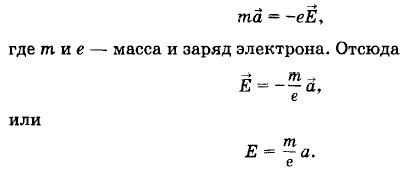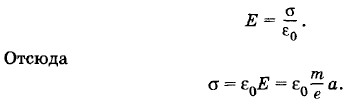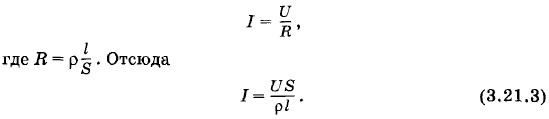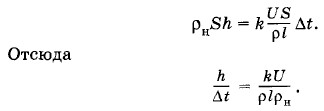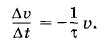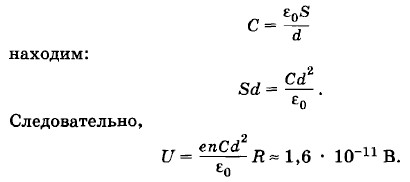|
|
|
|
|
Глава 3. Электрический ток в различных средах § 3.21. Примеры решения задачПри решении задач на материал этой главы к формулам, которыми мы пользовались в предыдущих двух главах, необходимо добавить закон электролиза в форме (3.5.6) или (3.5.8). Кроме того, надо четко представлять себе природу электрического тока в различных средах. Задача 1
Металлический прямоугольный параллелепипед (брусок), ребра которого имеют длину d, b, с (d >> с; b >> с), движется с ускорением Решение. При ускоренном движении бруска свободные электроны «отстают» и накапливаются на задней его грани. В результате задняя грань заряжается отрицательно, а передняя — положительно, и между этими гранями внутри бруска возникает электрическое поле. Перераспределение свободных электронов внутри бруска закончится тогда, когда возникшее электрическое поле будет в состоянии сообщать электронам ускорение Согласно второму закону Ньютона
Поверхностную плотность электрических зарядов на передней и задней гранях найдем из формулы напряженности поля между обкладками плоского конденсатора
Задача 2В электролитической ванне происходит покрытие детали никелем. Зная напряжение U между электродами, удельное сопротивление раствора электролита ρ, расстояние l между электродами, найдите скорость покрытия (т. е. скорость увеличения толщины h слоя никеля). Электрохимический эквивалент никеля k, плотность никеля — ρн. Решение. Согласно закону электролиза m = kIΔt. (3.21.1) Масса никеля, выделившегося при электролизе, m = ρнSh, (3.21.2) где S — площадь поверхности покрываемой никелем детали. Сила тока в растворе электролита, согласно закону Ома,
Подставляя выражение для массы (3.21.2) и силы тока (3.21.3) в соотношение (3.21.1), получим:
Задача 3
К источнику высокого напряжения через резистор сопротивлением R = 103 Ом подключен конденсатор емкостью С = 10-11 Ф с расстоянием между пластинами d = 3 мм (рис. 3.64). Воздух в пространстве между пластинами конденсатора ионизуется рентгеновскими лучами так, что в 1 см3 ежесекундно образуется n = 104 пар ионов. Заряд каждого иона равен по модулю заряду электрона. Найдите падение напряжения на резисторе R, считая, что все ионы достигают пластин конденсатора, не успевая рекомбинировать. Решение. По закону Ома искомое падение напряжения U = IR где I — сила тока в цепи. Ток одинаков во всех сечениях три конденсатора. На положительную пластину этот ток обусловлен только отрицательными ионами, а на отрицательную — только положительными. Через произвольное сечение внутри конденсатора проходит некоторая доля как положительных, так и отрицательных ионов. Сила тока I = enSd, где е — заряд электрона, a S — площадь пластин. Из формулы для емкости плоского конденсатора
|
|
|



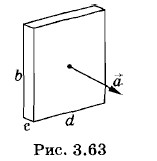
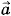 в направлении, параллельном меньшему ребру (рис. 3.63). Найдите напряженность электрического поля, возникающего вследствие ускоренного движения металлического бруска, а также поверхностную плотность электрических зарядов на боковых гранях бруска, перпендикулярных направлению ускорения.
в направлении, параллельном меньшему ребру (рис. 3.63). Найдите напряженность электрического поля, возникающего вследствие ускоренного движения металлического бруска, а также поверхностную плотность электрических зарядов на боковых гранях бруска, перпендикулярных направлению ускорения.
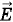 поля внутри бруска при этом достигнет максимального значения.
поля внутри бруска при этом достигнет максимального значения.