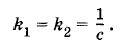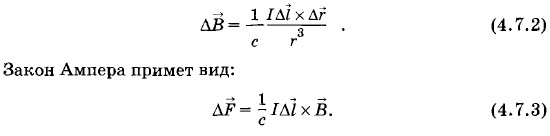|
|
|
|
|
Глава 4. Магнитное поле токов § 4.7. Системы единиц для магнитных взаимодействий
Абсолютная система единицВ принципе можно было бы установить единицу магнитной индукции из закона Био—Савара—Лапласа (4.5.4) или его следствия (4.5.5), положив коэффициент пропорциональности k1 = 1. Но в этом случае единицы напряженности электрического поля Основная идея абсолютной системы в том, чтобы единицы физических величин, характеризующих электрическое и магнитное поля, имели одинаковые наименования. Поэтому эту систему иногда называют симметричной. Электродинамическая постояннаяБудем исходить из формулы (4.6.3) для взаимодействия токов. Положить в этой формуле k = 1 нельзя, так как единицы для всех величин, входящих в эту формулу, уже установлены. Коэффициент k — размерная (именованная) величина. Найдем единицу k из формулы (4.6.3):
Здесь использована единица силы, определяемая законом Кулона: Как найти его численное значение? Для этого в принципе надо измерить силу F взаимодействия параллельных токов. Тогда, зная I1, I2, d и l, можно вычислить значение с. Здесь нас подстерегает неожиданность: электродинамическая постоянная с равна скорости света в вакууме: с = 3 • 1010 см/с. (4.7.1) Поразительный фактПостоянная с имеет глубокий физический смысл. Именно значение постоянной с натолкнуло в свое время Максвелла на гипотезу об электромагнитной природе света. Удивительно, что скорость света можно определить, измеряя силу взаимодействия постоянных токов. Законы магнитных взаимодействий в абсолютной системе единиц (в системе Гаусса)При построении абсолютной системы, далее, полагается, что
Такой выбор коэффициентов k1 и k2 обеспечивает, как вы
можете в этом убедиться сами, совпадение единиц Окончательно закон Био—Савара—Лапласа в системе Гаусса запишется так:
|
|
|



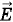 и магнитной индукции
и магнитной индукции 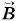 были бы различными. Единица напряженности
были бы различными. Единица напряженности 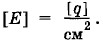 Здесь квадратные скобки означают, что речь идет о единицах. Указанная выше единица вытекает из выражения для напряженности электрического поля точечного заряда. Единица же магнитной индукции, как следует из формулы (4.5.5), при k1 = 1 иная:
Здесь квадратные скобки означают, что речь идет о единицах. Указанная выше единица вытекает из выражения для напряженности электрического поля точечного заряда. Единица же магнитной индукции, как следует из формулы (4.5.5), при k1 = 1 иная: 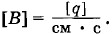
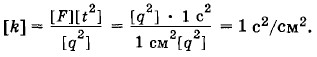
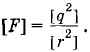 Теперь вместо k введем новый коэффициент пропорциональности:
Теперь вместо k введем новый коэффициент пропорциональности:  Новый коэффициент с часто называют электродинамической постоянной. Она выражается в таких же единицах, как и скорость: [с] = 1 см/с.
Новый коэффициент с часто называют электродинамической постоянной. Она выражается в таких же единицах, как и скорость: [с] = 1 см/с.