|
|
|
|
|
Глава 4. Магнитное поле токов § 4.9. Действие магнитного поля на движущийся заряд. Сила Лоренца
Сила ЛоренцаСилу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого нидерландского физика X. Лоренца, основателя электронной теории строения вещества. Эту силу можно найти с помощью закона Ампера. Она определяется как отношение силы Δ
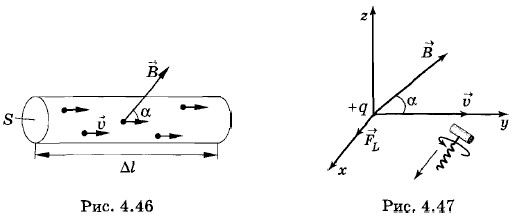
Рассмотрим отрезок тонкого прямого провода с током (рис. 4.46). Пусть длина отрезка Δl и площадь поперечного сечения S настолько малы, что вектор магнитной индукции Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц n и модулем скорости их упорядоченного движения I = qnυS. (4.9.2) Согласно закону Ампера (4.7.9) сила, действующая на элемент тока
Подставляя в это выражение значение силы тока (4.9.2), получим:
Векторы
где N = nSΔl — число заряженных частиц в рассматриваемом участке провода. На каждую заряженную частицу со стороны магнитного поля действует сила Лоренца
Модуль силы Лоренца, согласно определению векторного произведения, равен: FL = qυB sin α, (4.9.4) где υ — угол между векторами Сила Лоретта перпендикулярна плоскости, содержащей векторы В системе единиц Гаусса сила Лоренца равна:
Электрическое поле действует на заряд q с силой
то полная сила
Часто силой Лоренца называют полную силу (4.9.6). Тогда силу, определяемую формулой (4.9.3), называют магнитной частью силы Лоренца.
|
|
|



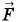 , действующей на участок проводника длиной Δl, к числу N упорядоченно движущихся заряженных частиц в этом участке проводника:
, действующей на участок проводника длиной Δl, к числу N упорядоченно движущихся заряженных частиц в этом участке проводника:

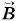 можно считать неизменным в пределах этого отрезка проводника.
можно считать неизменным в пределах этого отрезка проводника.
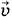 формулой (2.2.7):
формулой (2.2.7):
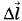 , в единицах СИ равна:
, в единицах СИ равна:
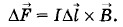

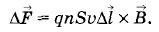
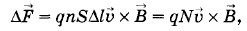


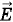 . Следовательно, если есть и электрическое поле и магнитное,
. Следовательно, если есть и электрическое поле и магнитное,