|
|
|
|
|
Глава 4. Магнитное поле токов Ответы к упражнению 8
4. В произвольной точке линии АВ любой малый элемент тока проводника АСВ создает магнитное поле, индукция которого перпендикулярна плоскости чертежа. Симметричный ему элемент проводника ADB создает такое же поле, но с индукцией, направленной в противоположную сторону. Суммарная индукция от двух любых симметрично расположенных элементов поэтому будет равна нулю. Следовательно, в произвольной точке на линии АВ индукция поля, созданного всем проводником, равна нулю, так как прямолинейные участки проводника также не создают поля на АВ.
7. а) Если токи I и i текут в одну сторону, то расстояние между шиной и проводом может быть: б) Если токи I и i текут в противоположных направлениях, то провод отталкивается от шины и будет в устойчивом равновесии на расстоянии
10. Контур притягивается к проводу с силой
16. Прямолинейное движение протона возможно в двух случаях: а) Вектор б) Векторы Так как е
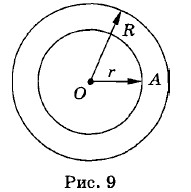
20. На рисунке 9 изображено сечение проводника. Определим магнитную индукцию
где I — сила тока, пронизывающего этот контур. Из соображений симметрии
где В — модуль искомой магнитной индукции. Выбранный контур охватывает часть проводника в виде цилиндра, радиус сечения которого равен r. Поэтому I = jπr2. Следовательно,
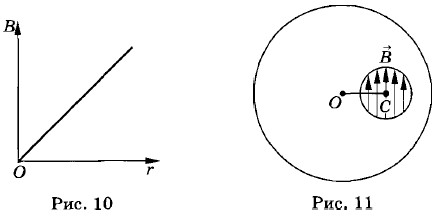
Из полученной формулы следует, что индукция магнитного поля внутри проводника с током прямо пропорциональна расстоянию от его оси. На оси проводника магнитная индукция равна нулю, а на его поверхности она максимальна. На рисунке 10 эта зависимость представлена графически. 21. 22. Магнитная индукция в произвольной точке внутри трубы равна нулю.
|
|
|



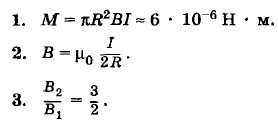
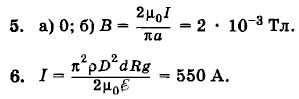
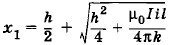 (устойчивое равновесие) или
(устойчивое равновесие) или 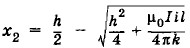 (неустойчивое равновесие). Если
(неустойчивое равновесие). Если 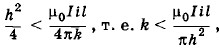 провод притянется к шине.
провод притянется к шине.
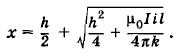
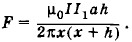
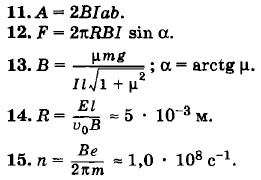
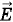 направлен вдоль траектории протона. Тогда вектор
направлен вдоль траектории протона. Тогда вектор 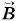 также должен быть направлен вдоль траектории и его модуль может быть любым, так как магнитное поле на частицу не будет действовать.
также должен быть направлен вдоль траектории и его модуль может быть любым, так как магнитное поле на частицу не будет действовать.
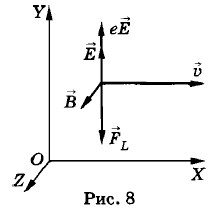
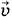 взаимно перпендикулярны, и сила, действующая на протон со стороны электрического поля, равна по модулю и противоположна по направлению силе Лоренца, действующей на протон со стороны магнитного поля (рис. 8).
взаимно перпендикулярны, и сила, действующая на протон со стороны электрического поля, равна по модулю и противоположна по направлению силе Лоренца, действующей на протон со стороны магнитного поля (рис. 8).
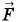 L = 0, то еЕ - eυB = 0 и
L = 0, то еЕ - eυB = 0 и 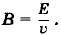
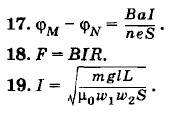
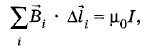
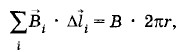
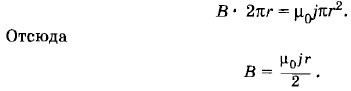
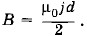 Поле однородно (рис. 11), линии индукции перпендикулярны
плоскости, проходящей через оси симметрии полости и проводника.
Поле однородно (рис. 11), линии индукции перпендикулярны
плоскости, проходящей через оси симметрии полости и проводника.