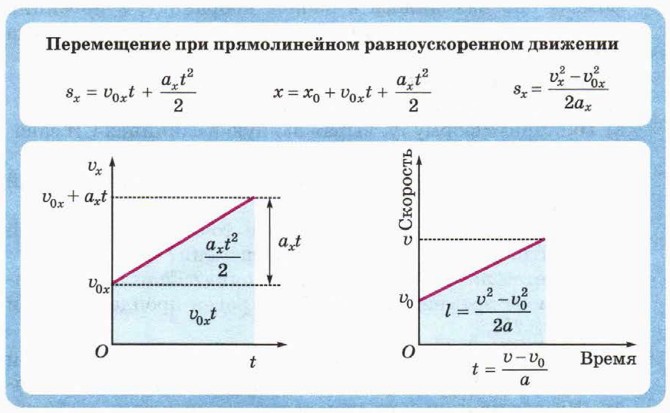
Дополнительные вопросы и задания к § 6: Перемещение при прямолинейном равноускоренном движении

Что мы узнали из § 6

Вопросы и задания к § 6

13. От движущегося поезда отцепляют последний вагон, после чего поезд движется равномерно, а вагон — с постоянным ускорением до полной остановки.

а) Изобразите на одном чертеже графики зависимости скорости от времени для поезда и вагона.

б) Во сколько раз путь, пройденный вагоном до остановки, меньше пути, пройденного поездом за то же время?

14. Отойдя от станции, электричка какое-то время ехала равноускоренно, затем в течение 1 мин — равномерно со скоростью 60 км/ч, после чего снова равноускоренно до остановки на следующей станции. Модули ускорений при разгоне и торможении были различны. Расстояние между станциями электричка прошла за 2 мин.

а) Начертите схематически график зависимости проекции скорости электрички от времени.

б) Используя этот график, найдите расстояние между станциями.

в) Какое расстояние проехала бы электричка, если бы на первом участке пути она разгонялась, а на втором — тормозила? Какова была бы при этом её максимальная скорость?

15. Тело движется равноускоренно вдоль оси х. В начальный момент оно находилось в начале координат, а проекция его скорости была равна 8 м/с. Через 2 с координата тела стала равной 12 м.

а) Чему равна проекция ускорения тела?

б) Постройте график зависимости υ_x(t).

в) Напишите формулу, выражающую в единицах СИ зависимость x(t).

г) Будет ли скорость тела равна нулю? Если да, то в какой момент времени?

д) Побывает ли тело второй раз в точке с координатой 12 м? Если да, то в какой момент времени?

е) Вернётся ли тело в начальную точку? Если да, то в какой момент времени, и чему будет равен пройденный при этом путь?

16. После толчка шарик вкатывается вверх по наклонной плоскости, после чего возвращается в начальную точку. На расстоянии b от начальной точки шарик побывал дважды через промежутки времени tх и t2 после толчка. Вверх и вниз вдоль наклонной плоскости шарик двигался с одинаковым по модулю ускорением.

а) Направьте ось х вверх вдоль наклонной плоскости, выберите начало координат в точке начального положения шарика и напишите формулу, выражающую зависимость x(t), в которую входят модуль начальной скорости шарика υ₀ и модуль ускорения шарика а.

б) Используя эту формулу и тот факт, что на расстоянии b от начальной точки шарик побывал в моменты времени t₁ и t₂, составьте систему двух уравнений с двумя неизвестными υ₀ и а.

в) Решив эту систему уравнений, выразите υ₀ и а через b, t₁ и t₂

г) Выразите весь пройденный шариком путь l через b, t₁ и t₂.

д) Найдите числовые значения υ₀, а и l при b = 30 см, t₁ = 1 с, t₂ = 2 с.

е) Постройте графики зависимости υ_x(t), sx(t), l(t).

ж) С помощью графика зависимости sx(t) определите момент, когда модуль перемещения шарика был максимальным.

<<< К началу Ответы и указания >>>